Chapitre 10 : Calcul Exact et Approché de Sommes de Séries

1 Calcul Exact de Sommes de Séries

Sous-sections

1 Calcul Exact de Sommes de Séries

Pour l'instant, on ne connait que la somme exacte des séries géométriques.

1.1 Sommation en dominos

On travaillera exclusivement sur un exemple. Soit la série : $\displaystyle\sum\limits_{n=1}^{+\infty}\dfrac{1}{n\left( n+1\right) }$ .
On montre facilement la convergence car $\dfrac{1}{n\left( n+1\right) } \underset{+\infty}{\sim}\dfrac{1}{n^{2}}$ qui est le terme général d'une série convergente par le critère de Riemann.
Pour le calcul de la somme, on revient en fait à la définition en calculant effectivement la somme partielle.
On a :

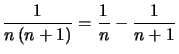
$\displaystyle \dfrac{1}{n\left( n+1\right) }=\dfrac{1}{n}-\dfrac{1}{n+1}$

d'où : 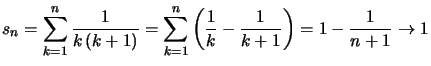$s_{n} =\displaystyle\sum\limits_{k=1}^{n}\dfrac{1}{k\left( k+1\right) } =\dis... ...=1}^{n}\left( \dfrac{1}{k}-\dfrac{1}{k+1}\right) =1-\dfrac{1}{n+1}\rightarrow1$ quand $n\rightarrow+\infty$ .
En effet, on peut procéder en dominos :

$\displaystyle u_{1}$	$\displaystyle =\dfrac{1}{1}-\dfrac{1}{2}$
$\displaystyle u_{2}$	$\displaystyle =\dfrac{1}{2}-\dfrac{1}{3}$
$\displaystyle u_{3}$	$\displaystyle =\dfrac{1}{3}-\dfrac{1}{4}$
$\displaystyle \cdots$	$\displaystyle =\cdots$
$\displaystyle u_{n}$	$\displaystyle =\dfrac{1}{n}-\dfrac{1}{n+1}$

Et en sommant, les termes se simplifient en dominos, et on obtient : 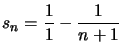$s_{n}=\dfrac{1}{1}-\dfrac{1}{n+1}$ .
On aurait aussi pu réindexer la somme, on reprend le même calcul : 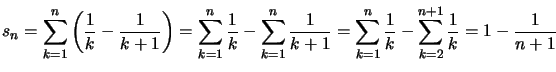$s_{n} =\displaystyle\sum\limits_{k=1}^{n}\left( \dfrac{1}{k}-\dfrac{1}{k+1}\ri... ...frac{1}{k}-\displaystyle\sum\limits_{k=2}^{n+1}\dfrac{1} {k}=1-\frac{1}{n+1}$ .

1.2 Utilisation de séries entières ou de séries de Fourier

On se reportera à ces chapitres que nous allons bientôt étudier pour calculer des sommes exactes de séries numériques.