Chapitre 10 : Calcul Exact et Approché de Sommes de Séries

2 Calcul Approché de Sommes de Séries

Sous-sections

2 Calcul Approché de Sommes de Séries

Il est quand même rare de savoir calculer facilement la somme exacte d'une série numérique.
Ce qui fait l'importance du calcul approché de ces sommes.

2.1 Principe général

On nous donne une série convergente 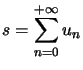$s=\displaystyle\sum\limits_{n=0}^{+\infty}u_{n}$ et un réel strictement positif $\varepsilon$ .
On cherche un rang tel que le reste d'ordre , $r_{n}$ vérifie $\left\vert r_{n}\right\vert \leqslant\varepsilon$ .
Ensuite, on prendra $s_{n}$ comme valeur approchée à $\varepsilon$ près de .
On va étudier les façons usuelles de chercher selon la série.
Sauf dans le premier cas, en général, l'énoncé guide vers la méthode à utiliser...

2.2 Série alternée répondant au critère spécial

Condition : La convergence de la série peut se montrer en utilisant le critère spécial des séries alternées.

C'est le cas le plus simple puisqu'on a un théorème.
Comme on sait que si $\displaystyle\sum u_{n}$ vérifie les conditions du critère spécial, $\left\vert r_{n}\right\vert \leqslant\left\vert u_{n+1}\right\vert$ , on cherche simplement tel que $\left\vert u_{n+1}\right\vert \leqslant\varepsilon$ et on calcule $s_{n}$ .
En plus, le théorème nous donne le signe de l'erreur qui est celui de $u_{n+1}$ .

Exemple : $s=\displaystyle\sum\limits_{n=1}^{+\infty}\dfrac{\left( -1\right) ^{n}}{n}$ à $10^{-2}$ près.
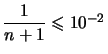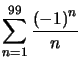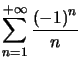Il nous suffit $\dfrac{1}{n+1}\leqslant10^{-2}$ , c'est à dire $n\geqslant99$ . $\displaystyle\sum\limits_{n=1}^{99}\dfrac{\left( -1\right) ^{n}}{n}$ est une valeur approchée à $10^{-2}$ près de $\displaystyle\sum\limits_{n=1}^{+\infty} \dfrac{\left( -1\right) ^{n}}{n}$ .
Il suffit de calculer cette somme.

2.3 Série comparable à une série géométrique positive

Condition : La convergence absolue de la série peut se montrer en utilisant le critère de d'Alembert.

C'est souvent la méthode la plus rapide quand elle est applicable.

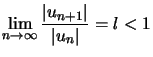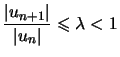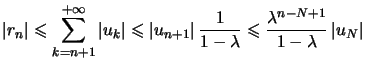Solution : $\lim\limits_{n\rightarrow\infty}\dfrac{\left\vert u_{n+1}\right\vert }{\left\vert u_{n}\right\vert }=l<1$ , d'où, à partir de , $\dfrac{\left\vert u_{n+1}\right\vert }{\left\vert u_{n}\right\vert }\leqslant\lambda<1$ , et donc, pour $n\geqslant N$ , $\left\vert r_{n}\right\vert \leqslant\displaystyle\sum\limits_{k=n+1}^{+\infty... ...mbda} \leqslant\dfrac{\lambda^{n-N+1}}{1-\lambda}\left\vert u_{N}\right\vert$ .
Ceci permet le bon rang en majorant cette quantité par $\varepsilon$ .
Ce rang sera bien sûr au moins égal à .

Exemple : On cherche 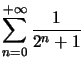$\displaystyle\sum\limits_{n=0}^{+\infty}\dfrac{1}{2^{n}+1}$ à $10^{-3}$ prés.
La convergence de cette série positive est facilement obtenue (par exemple) par équivalence avec une série géométrique.
On a 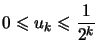$0\leqslant u_{k}\leqslant\dfrac{1}{2^{k}}$ qui est le terme général d'une série convergente, et donc : $0\leqslant\displaystyle\sum\limits_{k=n+1}^{+\infty}u_{k}\leqslant\displaystyl... ...\dfrac{1}{2^{k}}=\dfrac{\dfrac{1}{2^{n+1}}} {1-\dfrac{1}{2}}=\dfrac{1}{2^{n}}.$
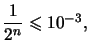Il suffit donc de chercher tel que $\dfrac{1}{2^{n}}\leqslant10^{-3},$ c'est à dire $2^{n}\geqslant10^{3}$ ou enfin $n\geqslant\dfrac{3\ln10} {\ln2}\simeq9,97$
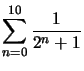Donc convient, $\displaystyle\sum\limits_{n=0}^{10}\dfrac{1}{2^{n}+1}$ est une valeur approchée à $10^{-3}$ prés de $\displaystyle\sum\limits_{n=0}^{+\infty }\dfrac{1}{2^{n}+1}.$
Il suffit donc de calculer cette somme.

2.4 Série comparable à une intégrale de Riemann

Condition : La convergence absolue se montre en utilisant le critère de Riemann.

Solution : On a pour $n\geqslant N$ , $\left\vert u_{n}\right\vert \leqslant\dfrac{K}{n^{\alpha }}$ avec $\alpha>1$ , et donc, pour $n\geqslant N$ , $\left\vert r_{n}\right\vert \leqslant\displaystyle\sum\limits_{k=n+1}^{+\infty... ...rt \leqslant K\displaystyle\sum\limits_{k=n+1}^{+\infty}\dfrac{1}{k^{\alpha}}$ .
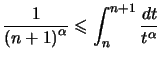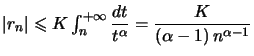Comme $\dfrac{1}{\left( n+1\right) ^{\alpha}}\leqslant\displaystyle\int_{n}^{n+1} \dfrac{dt}{t^{\alpha}}$ , on obtient : $\left\vert r_{n}\right\vert \leqslant K\int_{n}^{+\infty}\dfrac{dt}{t^{\alpha} }=\dfrac{K}{\left( \alpha-1\right) n^{\alpha-1}}$ .
Ceci permet le bon rang en majorant cette quantité par $\varepsilon$ .
Ce rang sera bien sûr au moins égal à .

Exemple : On cherche 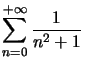$\displaystyle\sum\limits_{n=0}^{+\infty}\dfrac{1}{n^{2}+1}$ à $10^{-3}$ prés. La convergence de cette série positive est facilement obtenue (par exemple) par comparaison avec une intégrale généralisée.
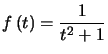En effet, définie par $f\left( t\right) =\dfrac{1}{t^{2}+1}$ est positive, décroissante et d'intégrale convergente à l'infini.
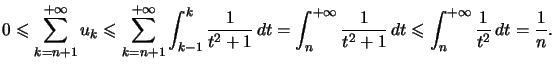
On a $0\leqslant u_{k}\leqslant\displaystyle\int_{k-1}^{k}\dfrac{1}{t^{2}+1}\,dt$ et donc $0\leqslant\displaystyle\sum\limits_{k=n+1}^{+\infty}u_{k}\leqslant\displaystyl... ...}\,dt\leqslant\displaystyle\int_{n}^{+\infty}\dfrac{1}{t^{2}}\,dt=\dfrac{1}{n}.$
Il suffit donc de chercher tel que $\dfrac{1}{n}\leqslant10^{-2},$ c'est à dire $n\geqslant100.$
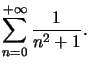
Donc convient, $\displaystyle\sum\limits_{n=0}^{100}\dfrac{1}{n^{2}+1}$ est une valeur approchée à $10^{-2}$ prés de $\displaystyle\sum\limits_{n=0}^{+\infty }\dfrac{1}{n^{2}+1}.$
Il suffit donc de calculer cette somme.