Chapitre 11 : Séries Entières

Une série de fonctions est une série du type :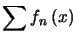$ \displaystyle\sum f_{n}\left( x\right) $.
Nous n'avons pas à notre programme d'étude générale des séries de fonctions.
Nous avons cependant à étudier deux types de séries de fonctions que sont les séries entières et les séries de Fourier.
On peut dire de toutes façons, qu'à $ x$ fixé, il s'agit d'une série numérique.
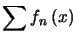Ainsi, l'ensemble des $ x$ pour lesquels la série$ \displaystyle\sum f_{n}\left( x\right) $ converge sera l'ensemble de définition de la somme.
Cette somme est donc une fonction de $ x$.
Se posent alors les problèmes usuels, cette fonction est-elle continue, dérivable ?...

© Christophe Caignaert - Lycée Colbert - Tourcoing