Chapitre 11 : Séries Entières

1 Séries Entières, Convergence

Sous-sections

1 Séries Entières, Convergence

1.1 Série entière

Définition : Une série entière de la variable est une série de la forme : $\displaystyle\sum a_{n}z^{n}$ . avec $z\in\mathbb{K}\left( \mathbb{K=R}\text{ ou }\mathbb{C}\right)$ et $a_{n}\in\mathbb{K}\left( \mathbb{K=R}\text{ ou }\mathbb{C}\right)$ .

Exemple : Un polynôme est un cas très particulier et sans intérêt de série entière.
Par contre, une série géométrique est le premier cas de série entière rencontré (sans le dire) dans le cadre des séries géométriques.

Pour une valeur de fixée à $z_{0}$ par exemple, la série $\displaystyle\sum a_{n}z_{0}^{n}$ est une série numérique.
Pour les valeurs de telles que la série converge, on définit donc, point par point, une fonction de la variable par : $f\left( z\right) =\displaystyle\sum_{n=0}^{+\infty}a_{n}z^{n}$ .
Un des objets de ce chapitre est d'étudier des propriétés de ces fonctions.
Quand la variable est réelle, on va plutôt la noter que .

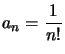Exemple : $\displaystyle\sum\limits_{n=0}^{+\infty}\dfrac{1}{n^{2}+1}z^{n}$ est donc une série entière où $a_{n}=\dfrac{1}{n^{2}+1}.$
Mais $\displaystyle\sum\limits_{n=0}^{+\infty}\dfrac{1}{\left( 2n\right) !}z^{2n}$ est aussi une série entière où $a_{n}=\dfrac{1}{n!}$ si est pair et $a_{n}=0$ si est impair...

1.2 Rayon de convergence

Théorème : Soit $\displaystyle\sum a_{n}z^{n}$ une série entière,
alors, il existe un réel positif ou « $+\infty$ » tel que : $R=\sup\left\{ r,r\in\mathbb{R}_{+}, \displaystyle\sum\left\vert a_{n}\right\vert r^{n}\text{ converge}\right\}$ . est appelé le rayon de convergence de $\displaystyle\sum a_{n}z^{n}$ .

Preuve. $I=\left\{ r,r\in\mathbb{R}_{+}, \displaystyle\sum\left\vert a_{n}\right\vert r^{n}\text{ converge}\right\}$ est un intervalle de $\mathbb{R}_{+}$ contenant 0, soit il est borné et admet alors une borne supérieure, soit il n'est pas borné et $R=+\infty$ . $\qedsymbol$

Exemple : Cherchons le rayon de convergence de $\displaystyle\sum\limits_{n=0}^{+\infty}z^{n}$
Soit $r\geqslant0,$ on sait que $\displaystyle\sum r^{n}$ ne converge que si et $\sup\left[ 0,1\right[ =1.$
On a donc

On reviendra rapidement sur les moyens de calcul pratique de ce rayon de convergence. Signalons qu'il s'agit d'une notion fondamentale dans l'étude des séries entières.

1.3 Disque ouvert de convergence

Définition : Soit $\displaystyle\sum a_{n}z^{n}$ une série entière, son rayon de convergence.
La boule ouverte de centre et de rayon , ou le plan complexe si $R=+\infty$ , est appelée disque ouvert de convergence ou intervalle ouvert de convergence selon que la variable est complexe ou réelle.
Ce disque est vide si .

Cette notion de disque ouvert de convergence se justifie par le théorème suivant :

Théorème : Soit $\displaystyle\sum a_{n}z^{n}$ une série entière, son rayon de convergence,

si $\left\vert z_{0}\right\vert <R$ alors $\displaystyle\sum a_{n}z_{0}^{n}$ converge absolument,
si $\left\vert z_{0}\right\vert >R$ alors $\displaystyle\sum a_{n}z_{0}^{n}$ diverge grossièrement, et
si $\left\vert z_{0}\right\vert =R$ , on ne sait rien à priori sur la convergence de la série.
Tout peut se produire.

La figure ci-dessous illustre le théorème.

$\includegraphics[ width=4in ]{serie-entiere}$

Preuve.
La première proposition découle directement de la définition du rayon de convergence, $\left\vert z_{0}\right\vert <R\Rightarrow\left\vert z_{0}\right\vert \in I$ , étant l'intervalle utilisé dans la démonstration de l'existence du rayon de convergence.
Pour la deuxième proposition, on a $\left\vert z_{0}\right\vert >R$ , supposons que la suite $\left( a_{n}z_{0}^{n}\right) _{n\in\mathbb{N}}$ soit bornée.
Alors il existe tel que : $\forall n\in\mathbb{N},\left\vert a_{n}\right\vert \left\vert z_{0}^{n}\right\vert \leqslant A$ .
Mais pour tel que $\left\vert z\right\vert <\left\vert z_{0}\right\vert$ , $\left\vert a_{n}\right\vert \left\vert z^{n}\right\vert =\left\vert a_{n}\righ... ...z_{0}}\right\vert ^{n}\leqslant A\left\vert \dfrac{z}{z_{0}}\right\vert ^{n}$
qui est le terme général d'une série géométrique convergente.
Ce qui prouve que $R\geqslant\left\vert z\right\vert$ pour $\left\vert z\right\vert <\left\vert z_{0}\right\vert$ , c'est à dire $R\geqslant\left\vert z_{0}\right\vert$ ,
ce qui est contraire à l'hypothèse.
La suite $\left( a_{n}z_{0}^{n}\right) _{n\in\mathbb{N}}$ n'est donc pas bornée, la série diverge (très) grossièrement. $\qedsymbol$

1.4 Recherche pratique du rayon de convergence

Remarque : On peut toujours travailler en module pour rechercher le rayon de convergence.
Une inégalité obtenue sur le rayon de convergence est toujours une inégalité large.
On applique quand on peut le théorème de d'Alembert sur la convergence des séries numériques.
Cependant on n'oubliera pas que ça n'est pas la seule méthode...

Par le théorème de d'Alembert.
On considère comme une série numérique en ne considérant pas les termes nuls, étant fixé non nul.
- Si le théorème de d'Alembert est applicable directement, est le $\left\vert z\right\vert$ tel qu'on soit dans le cas douteux, c'est à dire tel que la limite est .
- Si la limite est toujours nulle, $R=+\infty$ .
- Si pour un $\left\vert z\right\vert$ donné, la limite est inférieure ou égale à , $R\geqslant\left\vert z\right\vert$
- Si pour un $\left\vert z\right\vert$ donné, la limite est supérieure ou égale à , $R\leqslant\left\vert z\right\vert$
Dans le cas où le théorème de d'Alembert ne fournit pas le résultat, on obtient des inégalités en utilisant le paragraphe précédent.
Si on a un tel que $\displaystyle\sum a_{n}z^{n}_0$ converge, alors $R\geqslant\left\vert z_0\right\vert$ , tandis que,
si on a un tel que $\displaystyle\sum a_{n}z^{n}_0$ diverge, alors $R\leqslant\left\vert z_0\right\vert$ .
Si on a un $z_{0}$ tel que $\displaystyle\sum a_{n}z_{0}^{n}$ est semi-convergente, alors $R=\left\vert z_{0}\right\vert$ .
En effet, comme on n'a ni convergence absolue, ni divergence grossière, le rayon de convergence ne peut être ni plus grand ni plus petit que $\left\vert z_{0}\right\vert$ .
Si on n'a pas pu conclure en utilisant ce qui précède, on applique l'un des théorèmes suivants :
Théorème : $R=\sup\left\{ r,r\in\mathbb{R}_{+}, \lim\limits_{n\rightarrow\infty}\left\vert a_{n}\right\vert r^{n}=0\right\}$
Théorème : $R=\sup\left\{ r,r\in\mathbb{R}_{+}\text{, la suite }\left( a_{n}r^{n}\right) \text{ est born\'{e}e}\right\}$
L'intérêt de ces théorèmes est qu'il suffit d'étudier la suite $\left( \left\vert a_{n}\right\vert r^{n}\right)$ pour déterminer le rayon de convergence.
Il est donc inutile d'étudier la série, ce qui est plus complexe.
Le premier résulte immédiatement de la convergence d'une série entière, on montre le second :
Preuve. On a $\lim\limits_{n\rightarrow\infty}\left\vert a_{n}\right\vert r^{n} =0\Rightarrow\left( \left\vert a_{n}\right\vert r^{n}\right)$ est bornée d'où $R\geqslant r$ , ce qui entraine
$\displaystyle R\geqslant\sup\left\{ r,r\in\mathbb{R}_{+}, \lim\limits_{n\rightarrow\infty }\left\vert a_{n}\right\vert r^{n}=0\right\}$
Si $\lim\limits_{n\rightarrow\infty}\left\vert a_{n}\right\vert r^{n}\neq0$ , la série diverge et donc $r\geqslant R$ . Ce qui achève la démonstration. $\qedsymbol$

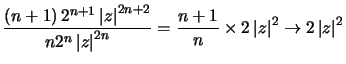Exemple : Cherchons le rayon de convergence de $\displaystyle\sum\limits_{n=0}^{+\infty}n2^{n}z^{2n}$ . $\dfrac{\left( n+1\right) 2^{n+1}\left\vert z\right\vert ^{2n+2}}{n2^{n}\left\v... ...\times2\left\vert z\right\vert ^{2}\rightarrow 2\left\vert z\right\vert ^{2}$ quand $n\rightarrow\infty$ , d'où $2R^{2}=1$ qui donne $R=\dfrac{1}{\sqrt{2}}$ .

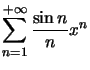Exemple : Cherchons le rayon de convergence de $\displaystyle\sum\limits_{n=1}^{+\infty}\dfrac{\sin n}{n}x^{n}$ .

Si $0\leqslant r<1$ , $\displaystyle\lim\limits_{n\rightarrow\infty}\dfrac{\sin n}{n}r^{n}=0$ , d'où $R\geqslant1$ car il est supérieur ou égal à tous les qui sont plus petits que 1.
Si , $\dfrac{\sin n}{n}r^{n}$ n'a pas de limite quand $n\rightarrow\infty$ , car $\dfrac{r^{n}}{n}\rightarrow+\infty$ et $\sin n$ n'a pas de limite.
Donc, $\dfrac{\sin n}{n}r^{n}\nrightarrow0$ et $R\leqslant1$ car il est inférieur ou égal à tous les qui sont plus grands que 1.
Et donc .