Chapitre 11 : Séries Entières

3 Somme d'une Série Entière de variable réelle

Sous-sections

3 Somme d'une Série Entière de variable réelle

On notera cette série entière : $\displaystyle\sum a_{n}x^{n}$ .

3.1 Intervalle de convergence, continuité

On a un théorème de continuité très simple qu'on va admettre.

Théorème : $\displaystyle\sum a_{n}x^{n}$ une série entière de rayon de convergence . On définit la fonction par : $f\left( x\right) =\displaystyle\sum\limits_{n=0}^{+\infty}a_{n}x^{n}$ .

Si $R=+\infty$ , $D_{f}=\mathbb{R}$ .
Si est fini, $\begin{displaymath}D_{f}=\left\{ \begin{array}[c]{l} \left] -R,R\right[ \\ \... ...right[ \\ \text{ou }\left[ -R,R\right] \end{array} \right. \end{displaymath}$

De plus, dans tous les cas, est continue sur $D_{f}$ .

3.2 Dérivation et intégration terme à terme

Les théorèmes ont encore des énoncés très simples et on va encore les admettre.

Théorème : $\displaystyle\sum a_{n}x^{n}$ une série entière de rayon de convergence . On définit la fonction par : $f\left( x\right) =\displaystyle\sum\limits_{n=0}^{+\infty}a_{n}x^{n}$ .
Alors est de classe $\mathcal{C}^{\infty}$ sur au moins $\left] -R,R\right[$ et $f^{\prime}\left( x\right) =\displaystyle\sum\limits_{n=1}^{+\infty}na_{n}x^{n-1}$ , est une série entière qui a, de plus, le même rayon de convergence .

Théorème : $\displaystyle\sum a_{n}x^{n}$ une série entière de rayon de convergence , convergente sur .
On définit la fonction par : $f\left( t\right) =\displaystyle\sum\limits_{n=0}^{+\infty}a_{n}t^{n}$ .
Alors $F\left( x\right) =\displaystyle\int_{0}^{x}f\left( t\right) dt=\displaystyle\sum\limits_{n=0} ^{+\infty}\dfrac{a_{n}}{n+1}x^{n+1}$ , est une série entière qui a encore le même rayon de convergence et qui converge partout où $\displaystyle\sum a_{n}x^{n}$ converge.

Remarque : En un mot, on peut dériver et intégrer terme à terme une série entière de variable réelle sur l'ouvert de convergence, ce qui ne change pas le rayon de convergence.
De plus, on peut intégrer terme à terme une série entière sur l'intervalle de convergence

3.3 Développements usuels

On peut voir sur le tableau ci-dessous les developpements usuels en dérie entière.

$\mathbf{f}$	D $_{f}$	DSE
$e^{x}$	$\mathbb{R}$	$\displaystyle\sum_{n=0}^{\infty}\dfrac{x^{n}}{n!}$	$+\infty$	$\mathbb{R}$
$\cos x$	$\mathbb{R}$	$\displaystyle\sum_{n=0}^{\infty}\left( -1\right) ^{n}\dfrac{x^{2n}}{\left( 2n\right) !}$	$+\infty$	$\mathbb{R}$
$\sin x$	$\mathbb{R}$	$\displaystyle\sum_{n=0}^{\infty}\left( -1\right) ^{n}\dfrac{x^{2n+1}}{\left( 2n+1\right) !}$	$+\infty$	$\mathbb{R}$
ch	$\mathbb{R}$	$\displaystyle\sum_{n=0}^{\infty} \dfrac{x^{2n}}{\left( 2n\right) !}$	$+\infty$	$\mathbb{R}$
sh	$\mathbb{R}$	$\displaystyle\sum_{n=0}^{\infty} \dfrac{x^{2n+1}}{\left( 2n+1\right) !}$	$+\infty$	$\mathbb{R}$
$\dfrac{1}{1+x}$	$\mathbb{R}\setminus\{-1\}$	$\displaystyle\sum _{n=0}^{\infty}\left( -1\right) ^{n}x^{n}$		$\left] -1,1\right[$
$\ln(1+x)$	$\left] -1,+\infty\right[$	$\displaystyle\sum_{n=1}^{\infty }\left( -1\right) ^{n+1}\dfrac{x^{n}}{n}$		$\left] -1,1\right]$
$\dfrac{1}{1-x}$	$\mathbb{R}\setminus\{1\}$	$\displaystyle\sum _{n=0}^{\infty}x^{n}$		$\left] -1,1\right[$
$\ln(1-x)$	$\left] -\infty,1\right[$	$\displaystyle-\sum_{n=1}^{\infty }\dfrac{x^{n}}{n}$		$\left[ -1,1\right[$
$\arctan x$	$\mathbb{R}$	$\displaystyle\sum_{n=0}^{\infty}\left( -1\right) ^{n}\dfrac{x^{2n+1}}{\left( 2n+1\right) }$		$\left[ -1,1\right]$
$(1+x)^{a}$	$\left] -1,+\infty\right[$	$1+\displaystyle\sum _{n=1}^{\infty}\dfrac{a(a-1)\ldots(a-n+1)}{n!}x^{n}$	ou $+\infty$ $\left( a\in\mathbb{N}\right)$

La série géométrique et l'exponentielle sont aussi valables pour une variable complexe.

Preuve.

Pour $e^{x}$ , on applique l'inégalité de Taylor-Lagrange à l'ordre en 0 : $\left\vert e^{x}-\displaystyle\sum\limits_{k=0}^{n}\dfrac{x^{k}}{k!}\right\ver... ...x\right\vert ^{n+1}}{\left( n+1\right) !}\times e^{\left\vert x\right\vert }$ .
Or $\lim\limits_{n\rightarrow\infty}\dfrac{\left\vert x\right\vert ^{n+1}}{\left( n+1\right) !}e^{\left\vert x\right\vert }=0$ , ce qui se montre facilement en montrant que la série converge.
D'où $\displaystyle\lim\limits_{n\rightarrow\infty}\left( e^{x}-\displaystyle\sum\limits_{k=0}^{n} \dfrac{x^{k}}{k!}\right) =0$ ce qui est le résultat annoncé.
Pour $\cos x$ , on utilise le même procédé : $\left\vert \cos x-\displaystyle\sum\limits_{k=0}^{n}\dfrac{\left( -1\right) ^{... ...eqslant\dfrac{\left\vert x\right\vert ^{2k+1} }{\left( 2k+1\right) !}\times1$ .
Or $\lim\limits_{n\rightarrow\infty}\dfrac{\left\vert x\right\vert ^{2k+1}}{\left( 2k+1\right) !}=0$ , ce qui se montre facilement en montrant que la série converge.
On conclut de la même façon.
Pour $\sin x$ , on utilise le même procédé : $\left\vert \sin x-\displaystyle\sum\limits_{k=0}^{n}\dfrac{\left( -1\right) ^{... ...eqslant\dfrac{\left\vert x\right\vert ^{2k+2} }{\left( 2k+2\right) !}\times1$ .
Or $\lim\limits_{n\rightarrow\infty}\dfrac{\left\vert x\right\vert ^{2k+2}}{\left( 2k+2\right) !}=0$ , ce qui se montre facilement en montrant que la série converge.
On conclut de la même façon.
Pour ch , on écrit que ch $x=\dfrac{e^{x}+e^{-x}}{2}$ , le résultat en découle immédiatement.
C'est la même chose pour sh $x=\dfrac{e^{x}-e^{-x}}{2}$
$\dfrac{1}{1+x}$ est somme d'une série géométrique, de même $\dfrac{1}{1-x}$ .
La démonstration a été faite dans le chapitre relatif aux séries numériques.
$\ln\left( 1+x\right)$ et $-\ln\left( 1-x\right)$ sont les primitives des précédentes qui s'annullent en 0.
On va montrer le prolongement à la borme pour $\ln\left( 1+x\right)$ , on l'admettra pour $-\ln\left( 1-x\right)$ .
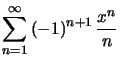On a la convergence de en de $\displaystyle\sum_{n=1}^{\infty }\left( -1\right) ^{n+1}\dfrac{x^{n}}{n}$ par application du critère spécial des séries alternées.
Ceci prouve la continuité de la somme de la série entière en 1.
Ainsi, la fonction et son développement en série entière sont :
- définies et égales sur $\left] -1,1\right[$ ,
- définies et continues toutes les deux en ,
on a ainsi l'égalité entre la fonction et la série entière en 1 et donc sur $\left] -1,1\right]$ .

Remarque : Ce procédé est très usuel pour « prolonger » l'égalité entre la fonction et son développement en série entière à une borne de l'intervalle de convergence.
Il est régulièrement utilisé par les problèmes.

$\arctan x$ est la primitive nulle en 0 de $\dfrac{1}{1+x^{2}}$ qui est aussi la somme d'une série géométrique.
La convergence en et en s'obtient encore par application du critère spécial.
L'égalité entre la fonction et la série entière en et en s'obtient encore en utilisant :
- l'égalité de la fonction et de la série entière sur $\left] -1,1\right[$ ,
- la continuité de la fonction et de la série entière en et .
Pour $\left( 1+x\right) ^{\alpha}$ , avec $x\in\left] -1,1\right[$ , on applique la formule de Taylor avec reste intégral :
$\displaystyle \left( 1+x\right) ^{\alpha}-\left( 1+\sum_{n=1}^{\infty}\dfrac {a(a-1)\ldots(a-n+1)}{n!}x^{n}\right)$
$\displaystyle =\int_{0}^{x}\dfrac{\left( x-t\right) ^{n}}{n!}a(a-1)\ldots(a-n)\left( 1+t\right) ^{\alpha-n-1}\,dt$

$\displaystyle =\dfrac{a(a-1)\ldots(a-n)}{n!}\int_{0}^{x}\left( \dfrac{x-t}{1+t}\right) ^{n}\left( 1+t\right) ^{\alpha-1}dt$

Or, on montre assez facilement que : $\left\vert \dfrac{x-t}{1+t}\right\vert \leqslant\left\vert x\right\vert$ , ce qui donne :
$\displaystyle \left\vert \left( 1+x\right) ^{\alpha}-\left( 1+\sum_{n=1}^{\inft... ...\vert ^{n}\left\vert \int_{0} ^{x}\left( 1+t\right) ^{\alpha-1}dt\right\vert$
On montre ensuite que cette quantité tend vers 0 en calculant l'intégrale et en montrant par application du théorème de d'Alembert que c'est le terme général d'une série convergente.
Ce qui est laissé au lecteur, qui prendra soin de séparer les cas et .

$\qedsymbol$

$\displaystyle \left( 1+x\right) ^{\alpha}-\left( 1+\sum_{n=1}^{\infty}\dfrac {a(a-1)\ldots(a-n+1)}{n!}x^{n}\right)$	$\displaystyle =\int_{0}^{x}\dfrac{\left( x-t\right) ^{n}}{n!}a(a-1)\ldots(a-n)\left( 1+t\right) ^{\alpha-n-1}\,dt$
	$\displaystyle =\dfrac{a(a-1)\ldots(a-n)}{n!}\int_{0}^{x}\left( \dfrac{x-t}{1+t}\right) ^{n}\left( 1+t\right) ^{\alpha-1}dt$