Chapitre 12 : Séries de Fourier

4 Espace Vectoriel $ \mathcal{C}_{T}\left( \mathbb{R}\right) $ des applications continues, $ T$-périodiques

Sous-sections

4 Espace Vectoriel $ \mathcal{C}_{T}\left( \mathbb{R}\right) $ des applications continues, $ T$-périodiques

4.1 Espace vectoriel $ \mathcal{C}_{T}\left( \mathbb{R}\right) $

Théorème :   $ \mathcal{C}_{T}(\mathbb{R})$, l'ensemble des applications continues,$ T$-périodiques, $ \mathbb{R}\rightarrow\mathbb{R}$ est un espace vectoriel réel.

Preuve. C'est clairement un sous-espace vectoriel de $ \mathcal{C}^{0}\left( \mathbb{R},\mathbb{R}\right) $ puisque

$ \qedsymbol$

4.2 Norme et produit scalaire sur $ \mathcal{C}_{T}\left( \mathbb{R}\right) $

Théorème :   Sur $ \mathcal{C}_{T}\left( \mathbb{R}\right) $ :    $ \left\langle f,g\right\rangle =\dfrac{1}{T} {\displaystyle\int_{\alpha}^{\alpha+T}} f(t)g(t)\,dt $     est un produit scalaire.
La norme associée est :$ \left\Vert f\right\Vert =\sqrt{\dfrac{1}{T}\displaystyle\int_{\alpha}^{\alpha+T}f^{2}\left( t\right) dt} $

Remarque :   Si les applications sont simplement continues par morceaux,$ \left\langle f,g\right\rangle =\dfrac{1}{T}\displaystyle {\displaystyle\int_{-T/2}^{T/2}} f(t)g(t)\,dt\quad$ est une forme bilinéaire symétrique positive.

Preuve.

$ \left\langle \cdot,\cdot\right\rangle $ est donc bien bilinéaire symétrique, définie positive, c'est un produit scalaire. $ \qedsymbol$

4.3 Famille orthogonale

Théorème :   La famille $ \left\{ \left( t\rightarrow\cos n\omega t\right) _{n\in \mathbb{N}},\left( t\rightarrow\sin n\omega t\right) _{n\in\mathbb{N}^{\ast }}\right\} $ est orthogonale pour ce produit scalaire.

Preuve. Il faut vérifier que ces applications sont 2 à 2 orthogonales.$ \dfrac{1}{T}\displaystyle\int_{0}^{T}\cos n\omega t\cos p\omega t\ \,dt=\dfrac... ...p\right) \omega t+\cos\left( n-p\right) \omega t\,dt=0\ \left( n\neq p\right) $


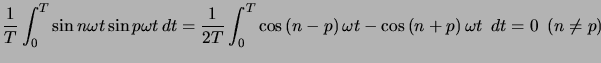
$ \dfrac{1}{T}\displaystyle\int_{0}^{T}\sin n\omega t\sin p\omega t\,dt=\dfrac{1... ...right) \omega t-\cos\left( n+p\right) \omega t\ \,dt=0\ \left( n\neq p\right) $


$ \dfrac{1}{T}\displaystyle\int_{0}^{T}\cos n\omega t\sin p\omega t\ \,dt=\dfrac... ...\int_{0}^{T}\sin\left( n+p\right) \omega t+\sin\left( p-n\right) \omega t\ \,dt$

        $ =-\dfrac{1}{2T}\left[ \dfrac{\cos\left( n+p\right) \omega t}{n+p} +\dfrac{\cos\left( p-n\right) \omega t}{p-n}\right] _{0}^{T}=0$
On a fait ce dernier calcul quand $ n\neq p$ mais le résultat est le même quand $ p=n$ car le deuxième $ \sin$ disparait directement. $ \qedsymbol$

4.4 Formule de Parseval

Théorème :   $ f:\mathbb{R}\rightarrow\mathbb{K}$, $ T$-périodique, continue par morceaux sur $ \mathbb{R}$, alors :

$\displaystyle \dfrac{1}{T} {\displaystyle\int_{-T/2}^{T/2}} \left\vert f^{2}(... ...ft( \left\vert a_{n}^{2}\right\vert +\left\vert b_{n}^{2}\right\vert \right) $

Si la fonction est réelle : 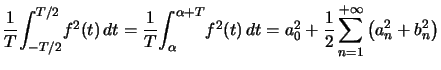   $ \dfrac{1}{T} {\displaystyle\int_{-T/2}^{T/2}} f^{2}(t)\,dt=\dfrac{1}{T} {\d... ...rac{1}{2}\displaystyle\sum_{n=1}^{+\infty}\left( a_{n}^{2} +b_{n}^{2}\right) $
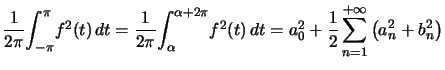
Si, de plus, $ f$ est 2$ \pi$-périodique,     $ \dfrac{1}{2\pi} {\displaystyle\int_{-\pi}^{\pi}} f^{2}(t)\,dt=\dfrac{1}{2\pi... ...rac{1}{2}\displaystyle\sum_{n=1}^{+\infty}\left( a_{n}^{2} +b_{n}^{2}\right) $

On va donner une interprétation géométrique pour les applications à valeur réelle. Soit :

$\displaystyle E_{n}=Vect\left( 1,\cos\omega t,\cos2\omega t,\ldots,\cos n\omega t,\sin\omega t,\sin2\omega t,\ldots,\sin n\omega t\right) $

dont une base orthonormale est :

$\displaystyle \left( 1,\sqrt{2}\cos\omega t,\sqrt{2}\cos2\omega t,\ldots,\sqrt{... ...rt{2}\sin\omega t,\sqrt{2}\sin2\omega t,\ldots,\sqrt{2}\sin n\omega t\right) $

La projection orthogonale $ f$ sur $ E_{n}$ est donc :

$\displaystyle p\left( f\right) \left( t\right) =\left\langle f,1\right\rangle ... ...{n}\left\langle f,\sqrt{2}\sin k\omega t\right\rangle \sqrt{2}\sin k\omega t $

Et donc, la norme de cette projection sur $ E_{n}$ est :$ \left\Vert p\left( f\right) \right\Vert ^{2}=\left\langle f,1\right\rangle ^{... ...splaystyle\sum_{k=1}^{n}\left\langle f,\sqrt{2}\sin k\omega t\right\rangle ^{2}$


        $ =\left( \dfrac{1}{T} {\displaystyle\int_{\alpha}^{\alpha+T}} f(t)\,dt\right)... ...t_{\alpha}^{\alpha+T}} f\left( t\right) \sqrt{2}\sin k\omega t\,dt\right) ^{2}$


        $ =\left( \dfrac{1}{T} {\displaystyle\int_{\alpha}^{\alpha+T}} f(t)\,dt\right)... ...style\int_{\alpha}^{\alpha+T}} f\left( t\right) \sin k\omega t\,dt\right) ^{2}$


        $ =a_{0}^{2}+\displaystyle\sum_{k=1}^{n}\dfrac{1}{2}a_{k}^{2}+\displaystyle\sum_{k=1}^{n}\dfrac{1} {2}b_{k}^{2}$

On voit bien que la formule de Parseval est la limite d'une égalité de normes.
Les $ \dfrac{1}{2}$ viennent du fait que les cosinus et sinus ne sont pas de norme 1 mais de norme $ \dfrac{1}{\sqrt{2}}$.

© Christophe Caignaert - Lycée Colbert - Tourcoing