Chapitre 12 : Séries de Fourier
5 Petits compléments
Sous-sections
On n'oubliera pas que pour  ,
, 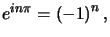
 ,
,  ,
, 
Les série de Fourier permettent de calculer facilement la somme de certaines séries numériques.
On considère donc : 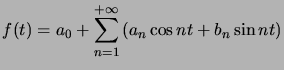 d'un coté et
d'un coté et  d'un autre. (cas de la période 2
d'un autre. (cas de la période 2 )
)
- Si les
 « ressemblent » aux
« ressemblent » aux  ou aux
ou aux  . Alors, on obtient la somme en prenant une valeur particulière de
. Alors, on obtient la somme en prenant une valeur particulière de  .
.
Le plus souvent, on essaye  ...
... - Si les
 « ressemblent » aux
« ressemblent » aux  ou aux
ou aux  . (avec en plus un module s'ils ne sont pas réels)
. (avec en plus un module s'ils ne sont pas réels)
Alors, on obtient la somme en utilisant la formule de Parseval.
On sait parfois que :  , ce résultat ayant été acquis sans le théorème de Dirichlet. (On obtient parfois un tel résultat en utilisant des séries entières en
, ce résultat ayant été acquis sans le théorème de Dirichlet. (On obtient parfois un tel résultat en utilisant des séries entières en  et
et 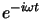 .)
.)
- Si
 est continue, on a bien la série de Fourier de
est continue, on a bien la série de Fourier de  .
. - Si
 n'est pas continue, rien ne prouve qu'il s'agit de la série de Fourier de
n'est pas continue, rien ne prouve qu'il s'agit de la série de Fourier de  .
.
Pour arriver au résultat, l'énoncé vous guide ... On peut par exemple prouver que cette série trigonométrique peut s'intégrer terme à terme sur une période, ce qui revient à l'inversion de signes et
et  .
.
Alors l'orthogonalité des  et
et  permettra de conclure qu'on a bien la série de Fourier de
permettra de conclure qu'on a bien la série de Fourier de  .
.
© Christophe Caignaert - Lycée Colbert - Tourcoing![]() ,
, ![]()
![]() ,
, ![]() ,
, ![]()
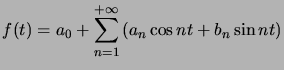 d'un coté et
d'un coté et  d'un autre. (cas de la période 2
d'un autre. (cas de la période 2![]() )
)  , ce résultat ayant été acquis sans le théorème de Dirichlet. (On obtient parfois un tel résultat en utilisant des séries entières en
, ce résultat ayant été acquis sans le théorème de Dirichlet. (On obtient parfois un tel résultat en utilisant des séries entières en ![]() et
et ![]() .)
.)