Chapitre 13 : Fonctions de plusieurs variables : Différentiabilité

1 Fonctions $ \mathbb{R}^{p}\rightarrow\mathbb{R}$, Dérivées Premières

Sous-sections

1 Fonctions $ \mathbb{R}^{p}\rightarrow\mathbb{R}$, Dérivées Premières

Dans cette partie, toutes les fonctions sont supposées définies sur un ouvert $ \mathcal{U}$ de $ \mathbb{R}^{p}$.
On travaillera toujours sur ce domaine $ \mathcal{U}$, sur lequel on a donc une application.

1.1 Application de classe $ \mathcal{C}^{1}$ sur $ \mathcal{U}$

Définition :   $ f:\mathbb{R}^{p}\rightarrow\mathbb{R}$, définie sur $ \mathcal{U}$, un ouvert de $ \mathbb{R}^{p}$,
on appelle dérivée partielle de$ f$ par rapport à la $ i^{\grave{e}me}$ variable, au point $ u=\left( x_{1}, x_{2},\ldots, x_{p}\right) :$

$\displaystyle \dfrac{\partial f}{\partial x_{i}}\left( x_{1}, x_{2},\ldots, ... ...t) -f\left( x_{1}, x_{2},\ldots, x_{i},\ldots, x_{p}\right) }{t-x_{i}} $

si cette limite existe.
Sinon, on dit que $ f$ n'admet pas de dérivée partielle par rapport à la $ i^{\grave{e}me}$ variable, au point $ u=\left( x_{1}, x_{2},\ldots, x_{p}\right) $.
On parle parfois de dérivée partielle première.

Remarque :   Quand il n'y a que 2 ou 3 variables on note souvent les dérivées partielles,

$\displaystyle \dfrac{\partial f}{\partial x}, \dfrac{\partial f}{\partial y},... ...ême }\dfrac{\partial g}{\partial \rho}, \dfrac{\partial g}{\partial \theta} $

Mais, on n'oubliera pas, en cas d'ambiguïté, qu'il s'agit des dérivées par rapport à la première, la seconde, ou la $ i^{\grave{e}me}$ variable...

Définition :   $ f$ est de classe $ \mathcal{C}^{1}$ sur $ \mathcal{U}$ un ouvert de$ \mathbb{R}^{p}\Leftrightarrow f$ admet $ p$ dérivées partielles continues sur $ \mathcal{U}$.
C'est à dire :    $ \forall i\in\left\{ 1, 2,\ldots, p\right\} , \dfrac{\partial f}{\partial x_{i}}$ est définie et continue sur $ \mathcal{U}$

1.2 Différentielle d'une application de classe $ \mathcal{C}^{1}$ sur $ \mathcal{U}$

Définition :   $ f:\mathbb{R}^{p}\rightarrow\mathbb{R}$, définie sur $ \mathcal{U}$, un ouvert de $ \mathbb{R}^{p}$, de classe $ \mathcal{C}^{1}$ sur $ \mathcal{U}$, on appelle différentielle de $ f$ en $ u=\left( x_{1},x_{2} ,\ldots,x_{p}\right) $, l'application linéaire notée $ df_{u} :\mathbb{R}^{p}\rightarrow\mathbb{R}$

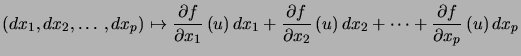
$\displaystyle \left( dx_{1},\, dx_{2},\ldots,\, dx_{p}\right) \mapsto\dfrac{\pa... ...ight) dx_{2}+\cdots+\dfrac{\partial f}{\partial x_{p}}\left( u\right) dx_{p} $

noté le plus souvent, pour alléger les notations :    $ df=\dfrac{\partial f}{\partial x_{1}}dx_{1}+\dfrac{\partial f}{\partial x_{2} }dx_{2}+\cdots+\dfrac{\partial f}{\partial x_{p}}dx_{p} $

Dans le cas de 2 ou 3 variables, on note souvent la différentielle de $ f$ en $ (x_{0},y_{0},z_{0}):$

$\displaystyle (dx,\, dy,\, dz)\longmapsto\dfrac{\partial f}{\partial x}(x_{0},\... ...,\, z_{0})\, dy+\dfrac{\partial f}{\partial z}(x_{0},\, y_{0},\, z_{0})\, dz $

ou bien :    $ df=\dfrac{\partial f}{\partial x}\, dx+\dfrac{\partial f}{\partial y} \, dy+\dfrac{\partial f}{\partial z}\, dz $

1.3 Développement limité à l'ordre 1 de $ f$ de classe$ \mathcal{C}^{1}$ sur $ \mathcal{U}$

Théorème :   $ f:\mathbb{R}^{p}\rightarrow\mathbb{R}$, définie sur $ \mathcal{U}$, un ouvert de $ \mathbb{R}^{p}$, de classe $ \mathcal{C}^{1}$ sur $ \mathcal{U}$, $ u=\left( x_{1},x_{2},\ldots,x_{p}\right) \in\mathcal{U}$.$ f$ admet un développement limité à l'ordre 1 en $ u$ et

$\displaystyle f\left( u+du\right) =f\left( u\right) +df_{u}\left( du\right) +o\left( du\right)$    avec $\displaystyle \lim_{\left\Vert du\right\Vert \rightarrow0} \dfrac{o\left( du\right) }{\left\Vert du\right\Vert }=0 $

C'est à dire pour 3 variables par exemple :

$\displaystyle f\left( x+dx,\, y+dy,\, z+dz\right) =f\left( x,\, y,\, z\right) +... ...dy+\dfrac {\partial f}{\partial z}(x,y,z)\, dz+o\left( dx,\, dy,\, dz\right) $

Preuve. On le montre pour 3 variables. La démonstration repose sur le théorème des accroissements finis.
Pour cela, il faut faire varier les variables une à la fois.

$\displaystyle f\left( x+dx,\, y+dy,\, z+dz\right) -f\left( x,\, y,\, z\right)$

$\displaystyle =f\left( x+dx,\, y+dy,\, z+dz\right) -f\left( x,\, y+dy,\, z+dz\right)$

   

 

$\displaystyle \qquad +f\left( x,\, y+dy,\, z+dz\right) -f\left( x,\, y,\, z+dz\right)$

   

 

$\displaystyle \qquad+f\left( x,\, y,\, z+dz\right) -f\left( x,\, y,\, z\right)$

   

 

$\displaystyle =\dfrac{\partial f}{\partial x}\left( x+\alpha \, dx,\, y+dy,\, z+dz\right)$

   

 

$\displaystyle \qquad+\dfrac{\partial f}{\partial y}\left( x,\, y+\beta \, dy,\,... ...z\right) +\dfrac{\partial f}{\partial z}\left( x,\, y,\, z+\gamma \, dz\right)$

   


avec $ \alpha,\beta,\gamma\in\left] 0,1\right[ $.
D'où, par continuité des dérivées partielles :

$\displaystyle f\left( x+dx,\, y+dy,\, z+dz\right) -f\left( x,\, y,\, z\right)$

$\displaystyle =\dfrac{\partial f}{\partial x}(x,\, y,\, z)\, dx+o\left( \left( dx,\, dy,\, dz\right) \right)$

   

 

$\displaystyle \qquad+\dfrac{\partial f}{\partial y}(x,\, y,\, z)\, dy+o\left( \... ...al f}{\partial z}(x,\, y,\, z)\, dz+o\left( \left( 0,\, 0,\, dz\right) \right)$

   


Il ne reste qu'à regrouper les $ o\left( \cdots\right) $ en un seul$ o\left( \left( dx,\, dy,\, dz\right) \right) $. $ \qedsymbol$

1.4 Gradient, dérivée selon un vecteur

Définition :   $ f:\mathbb{R}^{p}\rightarrow\mathbb{R}$, définie sur $ \mathcal{U}$, un ouvert de $ \mathbb{R}^{p}$, de classe $ \mathcal{C}^{1}$ sur $ \mathcal{U}$,    $ u=\left( x_{1}, x_{2},\ldots, x_{p}\right) \in\mathcal{U}$
On appelle gradient de $ f$ en $ u$, noté $ \overrightarrow {Grad_{u}\left( f\right) }$ le vecteur : \begin{displaymath}\left( \begin{array}[c]{c} \dfrac{\partial f}{\partial x_{1... ...artial f}{\partial x_{p}}\left( u\right) \end{array} \right) \end{displaymath}

Ce gradient a une grande importance dans l'étude des courbes d'équation $ f\left( x, y\right) =0$ ou des surfaces d'équation$ f\left( x, y, z\right) =0$ dans un repère orthonormal.

Définition :   $ f:\mathbb{R}^{p}\rightarrow\mathbb{R}$, définie sur $ \mathcal{U}$, un ouvert de $ \mathbb{R}^{p}$, de classe $ \mathcal{C}^{1}$ sur $ \mathcal{U}$,    $ u=\left( x_{1},x_{2},\ldots,x_{p}\right) \in\mathcal{U}$
On appelle dérivée de $ f$ suivant le vecteur\begin{displaymath}\overrightarrow{V}:\left( \begin{array}[c]{c} v_{1}\\ v_{2}\\ \vdots\\ v_{p} \end{array} \right) \end{displaymath} en $ u$ le produit scalaire

$\displaystyle \overrightarrow{Grad_{u}\left( f\right) }\cdot\overrightarrow{V}... ...\right) v_{2}+\cdots+\dfrac{\partial f}{\partial x_{p}}\left( u\right) v_{p} $

1.5 Algèbre $ \mathcal{C}^{1}\left( \mathcal{U},\mathbb{R}\right) $

Théorème :   L'ensemble des applications de classe $ \mathcal{C}^{1}$ sur $ \mathcal{U}$ un ouvert de $ \mathbb{R}^{p}$, à valeur réelle, muni de
\begin{displaymath} % latex2html id marker 3963 \left\{ \begin{array}[c]{c} \t... ... \text{Le produit de deux applications} \end{array} \right\} \end{displaymath} a une structure d'algèbre commutative.

Preuve. On montre que c'est une sous-algèbre de $ \mathcal{C}^{0}\left( \mathcal{U},\mathbb{R}\right) $. Clairement, $ \mathcal{C}^{1}\left( \mathcal{U},\mathbb{R}\right) $

$ \qedsymbol$

1.6 Différentielle et dérivées partielles de fonctions composées

On écrit le théorème pour une fonction de 3 variables. L'énoncé pour une fonction de $ p$ variables s'en déduit facilement.

Théorème :   \begin{displaymath}\left. \begin{array}[c]{r} x, y, z:\mathbb{R}\rightarro... ...), y(t), z(t)\right) \end{array} \right\} \Rightarrow F\end{displaymath} est de classe $ \mathcal{C}^{1}$ sur $ I$, et :

$\displaystyle \forall t\in I,\quad F^{\prime}(t)=\dfrac{\partial f}{\partial x}... ...tial f}{\partial y}y^{\prime}(t)+\dfrac{\partial f}{\partial z}z^{\prime}(t) $

Ou encore, en utilisant la notation différentielle :    $ \dfrac{dF}{dt}=\dfrac{\partial f}{\partial x}\, \dfrac{dx}{dt}+\dfrac{\partial... ...{\partial y}\, \dfrac{dy}{dt}+\dfrac{\partial f}{\partial z}\, \dfrac{dz}{dt} $
Bien sûr, toutes les dérivées partielles sont prises en $ \left( x(t), y(t), z(t)\right) $ et les dérivées en $ t$.

Preuve. On écrit la démonstration pour une fonction de 2 variables seulement !

$\displaystyle F\left( t+dt\right) -F\left( t\right)$

$\displaystyle =f\left( x(t+dt),\, y(t+dt)\right) -f\left( x(t),\, y(t)\right)$

   

 

$\displaystyle =f\left( x\left( t\right) +\dfrac{dx}{dt}\, dt+o\left( dt\right)... ...t) +\dfrac{dy}{dt}\, dt+o\left( dt\right) \right) -f\left( x(t),\, y(t)\right)$

   

 

$\displaystyle =\dfrac{\partial f}{\partial x}\times\left( \dfrac{dx}{dt}\, dt+o... ...tial f}{\partial y}\times\left( \dfrac {dy}{dt}\, dt+o\left( dt\right) \right)$

   

 

$\displaystyle +o\left( \dfrac{dx}{dt}\, dt+o\left( dt\right) ,\dfrac{dy}{dt}\, dt+o\left( dt\right) \right)$

   

 

$\displaystyle =\dfrac{\partial f}{\partial x}\, \dfrac{dx}{dt}+\dfrac{\partial ... ...+\dfrac{\partial f}{\partial y}\, o\left( dt\right) \right) +o\left( dt\right)$

   

 

$\displaystyle =\dfrac{\partial f}{\partial x}\, \dfrac{dx}{dt}+\dfrac{\partial f}{\partial y}\, \dfrac{dy}{dt}+o\left( dt\right)$

   


$ \qedsymbol$

Théorème :   On écrit ce théorème pour la composée de fonctions de plusieurs variables avec 2 et 3 variables.
Ceci est bien sûr arbitraire, le théorème s'applique avec $ p$ et $ q$ variables...\begin{displaymath}\left. \begin{array}[c]{r} f:\mathbb{R}^{3}\rightarrow\math... ...) , w\left( x, y\right) \right) \end{array} \right. \quad\end{displaymath} est de classe $ \mathcal{C}^{1}$ sur $ \mathcal{V}$ et :

$\displaystyle \dfrac{\partial F}{\partial x}$

$\displaystyle =\dfrac{\partial f}{\partial u} \dfrac{\partial u}{\partial x... ... v}{\partial x}+\dfrac{\partial f}{\partial w} \dfrac{\partial w}{\partial x}$

   

$\displaystyle \dfrac{\partial F}{\partial y}$

$\displaystyle =\dfrac{\partial f}{\partial u} \dfrac{\partial u}{\partial y... ... v}{\partial y}+\dfrac{\partial f}{\partial w} \dfrac{\partial w}{\partial y}$

   


On a aussi changé les notations parce qu'il faut pouvoir s'adapter !

Preuve. Quand on fixe $ y$, on se retrouve exactement dans les hypothèses du théorème précédent.
Ce qui donne $ \dfrac{\partial F}{\partial x}$. De même, on fixe $ x$ pour obtenir $ \dfrac{\partial F}{\partial y}$. $ \qedsymbol$


© Christophe Caignaert - Lycée Colbert - Tourcoing