Chapitre 13 : Fonctions de plusieurs variables : Différentiabilité

4 Fonctions Vectorielles $ \mathbb{R}\rightarrow$ $ \mathbb{R}^{p}$

Sous-sections

4 Fonctions Vectorielles $ \mathbb{R}\rightarrow$ $ \mathbb{R}^{p}$

4.1 Dérivée d'une fonction $ \mathbb{R}\rightarrow$$ \mathbb{R}^{p}$, classe $ \mathcal{C}^{k}$

Définition :   $ F:\mathbb{R}\rightarrow$ $ \mathbb{R}^{p}$, définie sur $ I$ un intervalle de $ \mathbb{R}$. avec :    $ F\left( x\right) =\left( f_{1}\left( x\right) , f_{2}\left( x\right) ,\ldots, f_{p}\left( x\right) \right) $     qu'on notera en ligne ou en colonne selon les cas.
On dit que $ F$ est de classe $ \mathcal{C}^{k}$ sur $ I\Leftrightarrow f_{1}, f_{2},\ldots, f_{p}$ sont de classe $ \mathcal{C}^{k}$ sur $ I$

On note d'ailleurs, pour $ x\in I$ :    $ F^{\prime}\left( x\right) =\left( f_{1}^{\prime}\left( x\right) , f_{2}^{\prime}\left( x\right) ,\ldots, f_{p}^{\prime}\left( x\right) \right) $     ou simplement :    $ F^{\prime}=\left( f_{1}^{\prime}, f_{2}^{\prime},\ldots, f_{p}^{\prime }\right) $
On fait de même pour les dérivées d'ordre supérieur.

Théorème :   $ \mathcal{C}^{k}\left( I,\mathbb{R}^{p}\right) $, l'ensemble des applications de classe $ \mathcal{C}^{k}$ définies sur $ I$, à valeur dans $ \mathbb{R}^{p}$, muni

est un espace vectoriel sur $ \mathbb{R}$.

Preuve. C'est encore une fois clairement un sous espace vectoriel de $ \mathcal{A} ^{k}\left( I,\mathbb{R}^{p}\right) $. $ \mathcal{C}^{k}\left( I,\mathbb{R}^{p}\right) $ est bien non vide (application nulle) et stable par combinaison linéaire.
Il suffit d'appliquer le théorème pour les applications à valeur réelle à chaque coordonnée. $ \qedsymbol$

4.2 Développement limité

Définition :   On dit que $ F$ admet un développement limité à l'ordre $ n$ en$ x_{0}$$ \Leftrightarrow$ chacune des $ p$ coordonnées de $ F$ admet un développement limité à l'ordre $ n$ en $ x_{0}$.

Théorème :   $ F$ de classe $ \mathcal{C}^{k}$ au voisinage de $ x_{0}$ admet un développement limité d'ordre $ k$ au voisinage de $ x_{0}$.
De plus, on a

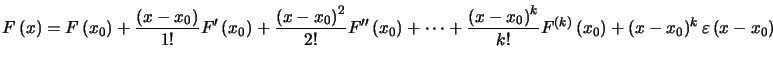
$\displaystyle F\left( x\right) =F\left( x_{0}\right) +\dfrac{\left( x-x_{0}\rig... ...ft( x_{0}\right) +\left( x-x_{0}\right) ^{k}\varepsilon\left( x-x_{0}\right) $

avec $ \varepsilon\left( x-x_{0}\right) \rightarrow0$ quand $ x\rightarrow x_{0}$

On notera que $ F, F^{\prime},\ldots, F^{\left( k\right) }$ et $ \varepsilon$ sont des fonctions vectorielles.
Cette formule s'appelle encore formule de Taylor-Young à l'ordre $ k$.

Preuve.$ F$ est de classe $ \mathcal{C}^{k}$ au voisinage de $ x_{0}$, d'où chaque$ f_{i}$ est de classe $ \mathcal{C}^{k}$ au voisinage de $ x_{0}$.
Chaque$ f_{i}$ admet donc un $ \mathrm{dl}_{k}$ au voisinage de $ x_{0}$ et enfin $ F$ admet un$ \mathrm{dl}_{k}$ au voisinage de $ x_{0}$. $ \qedsymbol$

4.3 Dérivée d'une fonction du type $ :x\rightarrow \lambda \left ( x\right ) F\left ( x\right ) $

Théorème :   Soit $ \lambda:I\rightarrow\mathbb{R}$ et $ F:I\rightarrow\mathbb{R}^{p}$ une fonction scalaire et une fonction vectorielle de classe $ \mathcal{C}^{k}$ sur$ I$. Alors \begin{displaymath}G:\left\{ \begin{array}[c]{rcl} I & \rightarrow & \mathbb{R... ... \lambda\left( x\right) F\left( x\right) \end{array} \right. \end{displaymath} est de classe $ \mathcal{C}^{k}$ sur $ I$.
De plus, on a la formule de Leibniz : 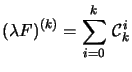   $ \left( \lambda F\right) ^{\left( k\right) }=\displaystyle\sum_{i=0}^{k} \mathcal{C} _{k}^{i}$ $ \lambda^{\left( i\right) }$ $ F^{\left( k-i\right) } $     avec la convention habituelle $ \lambda^{\left( 0\right) }=\lambda$ et$ F^{\left( 0\right) }=F$.

Preuve. On applique les théorèmes correspondants à chacune des coordonnées $ :x\rightarrow\lambda\left( x\right) f_{j}\left( x\right) $. $ \qedsymbol$

4.4 Dérivée d'un produit scalaire, d'un produit vectoriel.

Le principe est simple, un produit scalaire, ou le produit vectoriel (dans ce cas, on est en dimension 3) se dérivent comme des produits.

Théorème :   Soit $ F,G:I\rightarrow\mathbb{R}^{p}$, deux fonctions vectorielles de classe$ \mathcal{C}^{k}$ sur $ I$. Soit \begin{displaymath}s:\left\{ \begin{array}[c]{rcl} I & \rightarrow & \mathbb{R... ...& F\left( x\right) G\left( x\right) \end{array} \right. \quad\end{displaymath}
Alors $ s$ est de classe $ \mathcal{C}^{k}$ sur $ I$.

$\displaystyle s^{\prime}\left( x\right)$

$\displaystyle =F^{\prime}\left( x\right) G\left( x\right) +F\left( x\right) G^{\prime}\left( x\right)$

   

$\displaystyle s^{\left( k\right) }\left( x\right)$

$\displaystyle =\sum_{i=0}^{k} \mathcal{C}_{k} ^{i} F^{\left( i\right) }\left( x\right) G^{\left( k-i\right) }\left( x\right)$

   


Preuve. On vérifie la formule pour $ s^{\prime}$.
Ensuite, il suffit de procéder par récurrence, comme on l'a fait lors de la dé monstration de la formule de Leibniz pour les fonctions à valeur réelle.

$\displaystyle s\left( x\right)$

$\displaystyle =f_{1}\left( x\right) g_{1}\left( x\right) +f_{2}\left( x\right) g_{2}\left( x\right) +\cdots+f_{p}\left( x\right) g_{p}\left( x\right)$

   

$\displaystyle s^{\prime}\left( x\right)$

$\displaystyle =f_{1}^{\prime}\left( x\right) g_{1}\left( x\right) +f_{1}\left(... ...ight) g_{p}\left( x\right) +f_{p}\left( x\right) g_{p}^{\prime}\left( x\right)$

   

 

$\displaystyle =\left( f_{1}^{\prime}\left( x\right) g_{1}\left( x\right) +\cdo... ...( x\right) +\cdots +f_{p}\left( x\right) g_{p}^{\prime}\left( x\right) \right)$

   

 

$\displaystyle =F^{\prime}\left( x\right) G\left( x\right) +F\left( x\right) G^{\prime}\left( x\right)$

   


$ \qedsymbol$

Théorème :   Soit $ F,G:I\rightarrow\mathbb{R}^{3}$, deux fonctions vectorielles de classe$ \mathcal{C}^{k}$ sur $ I$. Soit \begin{displaymath}V:\left\{ \begin{array}[c]{rcl} I & \rightarrow & \mathbb{R... ...t( x\right) \wedge G\left( x\right) \end{array} \right. \quad\end{displaymath}
Alors $ V$ est de classe $ \mathcal{C}^{k}$ sur $ I$.

$\displaystyle V^{\prime}\left( x\right)$

$\displaystyle =F^{\prime}\left( x\right) \wedge G\left( x\right) +F\left( x\right) \wedge G^{\prime}\left( x\right)$

   

$\displaystyle V^{\left( k\right) }\left( x\right)$

$\displaystyle =\sum_{i=0}^{k} \mathcal{C}_{k} ^{i} F^{\left( i\right) }\left( x\right) \wedge G^{\left( k-i\right) }\left( x\right)$

   


Preuve. On vérifie la formule pour $ V^{\prime}$.
Ensuite, il suffit de procéder par récurrence.

$\displaystyle V\left( x\right)$

$\displaystyle =f_{1}\left( x\right) \wedge g_{1}\left( x\right) +\cdots+f_{p}\left( x\right) \wedge g_{p}\left( x\right)$

   

$\displaystyle V^{\prime}\left( x\right)$

$\displaystyle =f_{1}^{\prime}\left( x\right) \wedge g_{1}\left( x\right) +f_{1... ..._{p}\left( x\right) +f_{p}\left( x\right) \wedge g_{p}^{\prime}\left( x\right)$

   

 

$\displaystyle =\left( f_{1}^{\prime}\left( x\right) \wedge g_{1}\left( x\right)... ...ght) +\cdots+f_{p}\left( x\right) \wedge g_{p}^{\prime}\left( x\right) \right)$

   

 

$\displaystyle =F^{\prime}\left( x\right) \wedge G\left( x\right) +F\left( x\right) \wedge G^{\prime}\left( x\right)$

   


$ \qedsymbol$

En résumé, dans tous les cas, un produit se dérive comme un produit.

© Christophe Caignaert - Lycée Colbert - Tourcoing