Chapitre 14 : Intégrales Doubles et Triples

1 Intégrales doubles

Sous-sections

1 Intégrales doubles

1.1 Description hiérarchique d'une partie fermée bornée de $ \mathbb{R}^{2}$

Définition :   On appelle description hiérarchique du domaine $ \Delta $ une partie fermée bornée de $ \mathbb{R}^{2}:$ l'existence de 2 réels $ a$ et$ b$ et de 2 applications continues sur $ \left[ a,b\right] $, notées $ u$ et $ v $ tels que $ a<b$ et $ \forall x\in\left[ a,b\right] $, $ u(x)\leqslant v(x)$, avec

\begin{displaymath} (x,y)\in\Delta\Leftrightarrow\left\{ \begin{array}[c]{l} ... ...right] \\ y\in\left[ u(x),v(x)\right] \end{array} \right. \end{displaymath}

Ce qui peut s'illustrer par la figure ci-dessous.

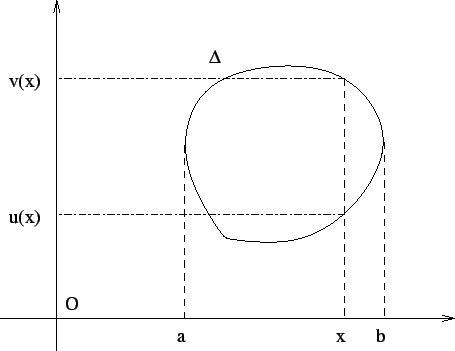
\includegraphics[

On fera attention à ne pas commettre l'erreur du débutant qui cherche les bornes extrèmes pour les 2 variables independament les unes des autres, et transforme tous les domaines en rectangle...

Exemple :   On va prendre le domaîne du plan défini par :    $ y\geqslant 0,\quad x\geqslant y, \quad x\leqslant 1$.
Il est élémentaire de faire une figure de ce domaîne, qui est un triangle.
En travaillant sur cette figure, on obtient facilement une description hiérarchique :    \begin{displaymath}\left\{ \begin{array}[c]{l} x\in\left[ 0,1\right] \\ y\in\left[ 0,x\right] \end{array} \right.\end{displaymath}

1.2 Intégrale double de $ f$ continue sur $ \Delta $, un fermé borné de $ \mathbb{R}^{2}$

Définition :   $ f$ continue sur $ \Delta $, un fermé borné de $ \mathbb{R}^{2}$, si on dispose d'une description hiérarchique de $ \Delta $, on appelle intégrale double de $ f$ sur $ \Delta:$

$\displaystyle I= {\displaystyle\iint_{\Delta}} f(x,y) dx dy= {\displayst... ...int_{a}^{b}} \left( {\displaystyle\int_{u(x)}^{v(x)}} f(x,y) dy\right) dx $

En un mot, on transforme cette intégrale double en 2 intégrales simples emboitées

Exemple :   On va intégrer la fonction $ \left( x,y\right) \rightarrow f\left( x,y\right) =xy$ sur \begin{displaymath}D:\left\{ \begin{array}[c]{c} x\geqslant0\\ y\geqslant0\\ x+y\leqslant1 \end{array} \right. \end{displaymath}
On cherche d'abord une description hiérarchique du domaîne \begin{displaymath}:\left\{ \begin{array}[c]{c} x\in\left[ 0,1\right] \\ y\in\left[ 0,1-x\right] \end{array} \right. ,\end{displaymath} ce qui donne :

$\displaystyle I$

$\displaystyle =\iint_{D}xy dx dy=\int_{0}^{1} \int_{0}^{1-x}xy dy dx$

   

$\displaystyle I$

$\displaystyle =\int_{0}^{1}\dfrac{x\left( 1-x\right) ^{2}}{2} dx=\left[ \dfrac... ...} dx=\left[ -\dfrac{\left( 1-x\right) ^{4}}{24}\right] _{0}^{1}=\dfrac{1}{24}$

   


1.3 Théorème de Fubini : inversion des bornes

Théorème :   Si on a par ailleurs :     \begin{displaymath} (x,y)\in\Delta\Leftrightarrow\left\{ \begin{array}[c]{l} ... ... y\right) ,\beta\left( y\right) \right] \end{array} \right. \end{displaymath} avec $ c<d$ et $ \forall y\in\left[ c,d\right] $, $ \alpha\left( y\right) \leqslant\beta\left( y\right) $, alors :

$\displaystyle I= {\displaystyle\iint_{\Delta}} f(x,y) dx dy= {\displaystyl... ...nt_{\alpha\left( y\right) }^{\beta\left( y\right) }} f(x,y) dx\right) d y $

Ceci est illustré sur la figure ci-dessous.

\includegraphics[

On peut changer l'ordre d'intégration, le calcul est différent, mais le résultat est le même.

1.4 Un cas particulier

On va se placer dans un cas très particulier puisque :    \begin{displaymath} (x,y)\in\Delta\Leftrightarrow\left\{ \begin{array}[c]{l} ... ...[ a,b\right] \\ y\in\left[ c,d\right] \end{array} \right. \end{displaymath} Le domaine est un rectangle.
Et d'autre part :    $ \forall(x,y)\in\Delta,\quad f\left( x,y\right) =\varphi\left( x\right) \psi\left( y\right) $
Alors, par linéarité des intégrales simples sur un intervalle :

$\displaystyle I$

$\displaystyle = {\displaystyle\iint_{\Delta}} f(x,y) dx dy= {\displaystyle\int_{a}^{b}} \left( {\displaystyle\int_{u(x)}^{v(x)}} f(x,y) dy\right) d x$

   

 

$\displaystyle = {\displaystyle\int_{a}^{b}} \left( {\displaystyle\int_{c}^{d... ...i\left( x\right) {\displaystyle\int_{c}^{d}} \psi\left( y\right) dy\right) dx$

   

 

$\displaystyle = {\displaystyle\int_{a}^{b}} \varphi\left( x\right) \left( {\... ...eft( y\right) dy\right) {\displaystyle\int_{a}^{b}} \varphi\left( x\right) dx$

   

 

$\displaystyle = {\displaystyle\int_{a}^{b}} \varphi\left( x\right) dx\times {\displaystyle\int_{c}^{d }} \psi\left( y\right) dy$

   


Ainsi, dans ce cas :    $ {\displaystyle\iint_{\Delta}} \varphi\left( x\right) \psi\left( y\right) dx ... ...\left( x\right) dx\times {\displaystyle\int_{c}^{d}} \psi\left( y\right) dy $

1.5 Propriétés

1.5.1 Linéarité

Théorème :   $ f,g$ continues sur $ \Delta $, un fermé borné de $ \mathbb{R}^{2}$, on dispose d'une description hiérarchique de $ \Delta $. $ \lambda$ et $ \mu$ deux réels.
Alors :

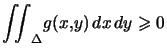
$\displaystyle {\displaystyle\iint_{\Delta}} \lambda f(x,y)+\mu$ $\displaystyle g\left( x,y\right) dx dy=\lambda$ $\displaystyle {\displaystyle\iint_{\Delta}} f(x,y) dx dy+\mu$ $\displaystyle {\displaystyle\iint_{\Delta}} g(x,y) dx dy\geqslant0 $

1.5.2 Positivité

Théorème :   $ f$ continue, positive, sur $ \Delta $, un fermé borné de $ \mathbb{R}^{2}$, on dispose d'une description hiérarchique de $ \Delta $.
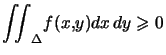
Alors :    $ {\displaystyle\iint_{\Delta}} f(x,y) dx dy \geqslant 0 $

1.5.3 Additivité selon les domaines

Théorème :   $ f$ continue, sur $ \Delta_{1}$ et $ \Delta_{2}$, deux fermés bornés de$ \mathbb{R}^{2}$, on dispose d'une description hiérarchique de $ \Delta_{1}$ et $ \Delta_{2}$.
De plus $ \Delta_{1}\cap\Delta_{2}$ est au plus une courbe. Alors :

$\displaystyle {\displaystyle\iint_{\Delta_{1}\cup\Delta_{2}}} f(x,y) dx d y=... ...a_{1}}} f(x,y) dx d y+ {\displaystyle\iint_{\Delta_{2}}} f(x,y) dx d y $

Cela permet d'exploiter d'éventuelles symétries (de la fonction et du domaine).

Théorème :   Si $ f$ est continue et positive sur $ \Delta $, avec, de plus, $ D \subset \Delta$, alors :

$\displaystyle \iint_Df(x,y) dx d y \leqslant \iint_{\Delta}f(x,y) dx d y $

1.6 Changement de variables

Théorème :   $ \varphi:\mathcal{U}\rightarrow\mathcal{V}$ de classe $ \mathcal{C}^{1}$,$ \mathcal{U}$ et $ \mathcal{V}$ deux ouverts de $ \mathbb{R}^{2}$.$ D$ et $ \Delta $ deux fermés bornés de $ \mathbb{R}^{2}$, $ D\subset \mathcal{U}$, et $ \Delta\subset\mathcal{V}$.
De plus $ \varphi\left( D\right) =\Delta$.
On suppose que les points de $ \Delta $ qui ont plusieurs antécédants sont de surface nulle.
On note : $ \left( x,y\right) =\varphi\left( u,v\right) $, $ \dfrac {D(x,y)}{D(u,v)}$ le jacobien de $ \varphi$ en $ \left( u,v\right) $, et,$ \left\vert \dfrac{D(x,y)}{D(u,v)}\right\vert$ la valeur absolue du jacobien.
Alors :$ {\displaystyle\iint_{D}} f(x,y) d x d y= {\displaystyle\iint_{\Delta}} g(u,v)\left\vert \dfrac{D(x,y)}{D(u,v)}\right\vert d u dv $

Remarque :   On notera la valeur absolue du jacobien et la pseudo-simplification.

On rappelle que :    \begin{displaymath} \dfrac{D(x,y)}{D(u,v)}=\left\vert \begin{array}[c]{cc} \d... ...u} & \dfrac{\partial y}{\partial v} \end{array} \right\vert \end{displaymath}

Remarque :   Notons qu'on fait un changement de variable :

Notons enfin que le domaine change et donc sa description hiérarchique aussi.

1.7 Changement de variables en coordonnées polaires

Théorème :   On pose \begin{displaymath}\left\{ \begin{array}[c]{l} x=\rho\cos\theta\\ y=\rho\sin\theta \end{array} \right. \end{displaymath} $ (x,y)\in D\Leftrightarrow(\rho,\theta)\in\Delta$, et$ f(x,y)=f\left( \rho\cos\theta,\rho\sin\theta\right) =g(\rho,\theta)$

$\displaystyle {\displaystyle\iint_{D}} f(x,y) dx d y= {\displaystyle\iint_{... ...elta}} f\left( \rho\cos\theta,\rho\sin\theta\right) \rho d\rho d\theta $

La figure ci-dessous explicite les coordonnées polaires.

\includegraphics[

Preuve. En effet\begin{displaymath} \dfrac{D(x,y)}{D(\rho,\theta)}=\left\vert \begin{array}[c]... ...ta & \rho\cos\theta \end{array} \right\vert =\rho\geqslant0 \end{displaymath} $ \qedsymbol$

Exemple :   On va intégrer la fonction $ \left( x,y\right) \rightarrow f\left( x,y\right) =xy$ sur \begin{displaymath}D:\left\{ \begin{array}[c]{c} x\geqslant0\\ y\geqslant0\\ x^{2}+y^{2}\leqslant1 \end{array} \right. \end{displaymath}
On cherche d'abord une description hiérarchique du domaîne en polaires\begin{displaymath}:\left\{ \begin{array}[c]{c} \theta\in\left[ 0,\pi/2\right] \\ \rho\in\left[ 0,1\right] \end{array} \right. ,\end{displaymath} ce qui donne, compte tenu que $ xy=\rho^{2}\cos\theta\sin\theta:$

$\displaystyle I$

$\displaystyle =\iint_{D}xy dx d y=\int_{0}^{\pi/2} \int_{0}^{1}\rho^{3}\cos\theta\sin \theta d\rho d\theta$

   

$\displaystyle I$

$\displaystyle =\int_{0}^{\pi/2}\cos\theta\sin\theta d\theta \int_{0}^{1}\rh... ...}\right] _{0}^{\pi/2} \left[ \dfrac{\rho^{4}}{4}\right] _{0}^{1}=\dfrac{1}{8}$

   



© Christophe Caignaert - Lycée Colbert - Tourcoing