Chapitre 14 : Intégrales Doubles et Triples

2 Intégrales triples

Sous-sections

2 Intégrales triples

2.1 Description hiérarchique de $ \Delta $, intégrale triple de$ f$ continue sur $ \Delta $ un fermé borné de $ \mathbb{R}^{3}$

$ \Delta $ un fermé borné de $ \mathbb{R}^{3}$, une description hiérarchique de $ \Delta $ est de la forme :

\begin{displaymath} (x,y,z)\in\Delta\Leftrightarrow\left\{ \begin{array}[c]{l}... ...\in\left[ \alpha(x,y),\beta(x,y)\right] \end{array} \right. \end{displaymath}

On peut avoir les variables dans un autre ordre, l'important est que les bornes de chacune ne soient définies qu'en fonction des précédentes.
On définit alors l'intégrale triple de $ f$ continue sur $ \Delta $ par :

$\displaystyle {\displaystyle\iiint_{\Delta}} f(x,y,z) dx d y d z= {\displa... ...splaystyle\int_{\alpha(x,y)}^{\beta(x,y)}} f(x,y,z) d z\right) dy\right) dx $

La figure ci-dessous donne une description hiérarchique du domaîne.

\includegraphics[

2.2 Changement de variables

Sous des hypothèses équivalentes à la dimension 2,$ (x,y,z)=\varphi(u,v,w)$, $ (x,y,z)\in D\Leftrightarrow(u,v,w)\in\Delta$, et$ f(x,y,z)=g(u,v,w)$, on a alors :

$\displaystyle {\displaystyle\iiint_{D}} f(x,y,z) dx d y d z= {\displaystyl... ...elta}} g(u,v,w)\left\vert \dfrac{D(x,y,z)}{D(u,v,w)}\right\vert du d v d w $

On notera la valeur absolue du jacobien et la pseudo-simplification.

2.3 Coordonnées cylindriques

\begin{displaymath} \left\{ \begin{array}[c]{l} x=\rho\cos\theta\\ y=\rho\s... ...\left( \rho\cos\theta,\rho\sin\theta\right) =g(\rho,\theta,z) \end{displaymath}

On regardera la figure ci-dessous.

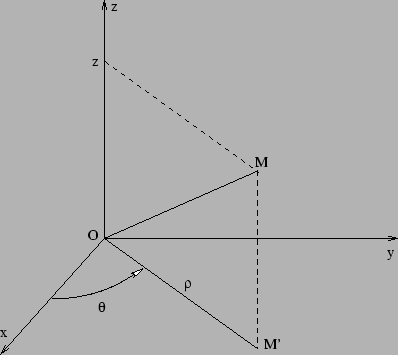
\includegraphics[

$\displaystyle {\displaystyle\iiint_{D}} f(x,y,z) dx d y d z= {\displaystyle\iiint_{\Delta}} g(\rho,\theta,z)\rho d\rho d \theta d z $

Le calcul du jacobien est facile $ \dfrac{D(x,y,z)}{D(\rho,\theta,z)}=\rho$ et on a encore $ \rho\geqslant0$.

2.4 Coordonnées sphériques

On notera sur la figure la définition des coordonnées sphériques.

Remarque :   Math : Les physiciens utilisent l'angle entre $ Oz$ et $ OM$ qui appartient donc à $ \left[ 0,\pi\right] $.
Dans la formule, au niveau de la valeur absolue du jacobien, ils échangent ainsi$ \sin\phi$ et $ \cos\phi$.
Attention, parfois, ils changent aussi le nom des angles...

\begin{displaymath} \left\{ \begin{array}[c]{l} x=\rho\cos\theta\cos\phi\\ ... ...eta,\phi)\in\Delta \text{, et } f(x,y,z)=g(\rho,\theta,\phi) \end{displaymath}

On regardera la figure ci-dessous.

\includegraphics[

$\displaystyle {\displaystyle\iiint_{D}} f(x,y,z) dx d y d z= {\displaystyl... ...int_{\Delta}} g(\rho,\theta,\phi)\rho^{2}\cos\phi d\rho d \theta d \phi $

Le calcul du jacobien est facile $ \dfrac{D(x,y,z)}{D(\rho,\theta,\phi)} =\rho^{2}\cos\phi$, et on a bien $ \cos\phi\geqslant0$.

© Christophe Caignaert - Lycée Colbert - Tourcoing