Chapitre 14 : Intégrales Doubles et Triples

3 Calculs divers

Sous-sections

3 Calculs divers

3.1 Aire ou volume de $\Delta$

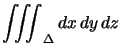Il suffit de calculer ${\displaystyle\iint_{\Delta}} d x d y$ pour l'aire d'une partie fermée bornée du plan et ${\displaystyle\iiint_{\Delta}} d x d y d z$ pour le volume d'une partie fermée bornée de l'espace.

3.2 Masse

Si on a $\mu\left( x,y,z\right)$ la masse volumique du solide en un point donné,

$\displaystyle M= {\displaystyle\iiint_{\Delta}} \mu\left( x,y,z\right) dx d y d z$

donne la masse. Pour une plaque, on peut faire un calcul équivalent avec la densité surfacique $\sigma\left( x,y\right)$ et une intégrale double,

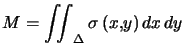
$\displaystyle M=\iint_{\Delta}\sigma\left( x,y\right) dx d y$

3.3 Centre d'inertie

Avec les mêmes notation, et de coordonnées $\left( x,y,z\right)$ on a :

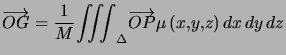
$\displaystyle \overrightarrow{OG}=\dfrac{1}{M} {\displaystyle\iiint_{\Delta}} \overrightarrow{OP}\mu\left( x,y,z\right) dx d y d z$

ou en densité surfacique :

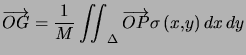
$\displaystyle \overrightarrow{OG}=\dfrac{1}{M}\iint_{\Delta}\overrightarrow{OP}\sigma\left( x,y\right) dx d y$

Ce qui donne pour la première coordonnée par exemple :

$\displaystyle x_{G}=\dfrac{1}{M} {\displaystyle\iiint_{\Delta}} x$ $\displaystyle \mu\left( x,y,z\right) dx d y d z$

ou encore, dans le cas d'une densité surfacique :

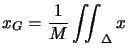
$\displaystyle x_{G}=\dfrac{1}{M}\iint_{\Delta}x$ $\displaystyle \sigma\left( x,y\right) dx d y$

3.4 Moments d'inertie

Pour un solide, un moment d'inertie peut se calculer par rapport à un point, une droite ou un plan qu'on appelle dans tous les cas .
On note $d\left( \left( x,y,z\right) ,A\right)$ la distance du point courant à .
Toujours avec les mêmes notations, on a :

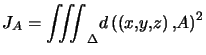
$\displaystyle J_{A}= {\displaystyle\iiint_{\Delta}} d\left( \left( x,y,z\right) ,A\right) ^{2}$ $\displaystyle \mu\left( x,y,z\right) dx d y d z$

On peut faire, une dernière fois, le même type de calcul pour une plaque :

$\displaystyle J_{A}=\iint_{\Delta}d\left( \left( x,y\right) ,A\right) ^{2}$ $\displaystyle \sigma\left( x,y\right) dx d y$

Pour un volume, le moment d'inertie par rapport à l'axe est donc :

$\displaystyle J_{Oz}= {\displaystyle\iiint_{\Delta}} \left( x^{2}+y^{2}\right)$ $\displaystyle \mu\left( x,y,z\right) dx d y d z$