Chapitre 15 : Courbes

1 Etude locale d'une courbe paramétrée

Sous-sections

1 Etude locale d'une courbe paramétrée

1.1 Tangente et demi-tangente en un point

La courbe $ C$ est l'ensemble des points $ M$ ou $ M\left( t\right) $ tels que$ \overrightarrow{OM}=\overrightarrow{F\left( t\right) }$ de coordonnées\begin{displaymath}\left( \begin{array}[c]{c} x\left( t\right) \\ y\left( t\right) \end{array} \right) \end{displaymath} ou \begin{displaymath}\left( \begin{array}[c]{c} x\left( t\right) \\ y\left( t\right) \\ z\left( t\right) \end{array} \right) \end{displaymath} selon les cas, $ t\in I$, un intervalle de $ \mathbb{R}$.
Sur cet intervalle, on suppose au minimum que $ \overrightarrow{F}$ est continue.

Définition :   $ M_{0}\left( t_{0}\right) \in C$, on dit que $ C$ admet une tangente en $ M_{0}$$ \Leftrightarrow$ la droite $ \left( M_{0}M\right) $, avec $ M=M\left( t\right) $, a une limite quand $ M\rightarrow M_{0}$, c'est à dire quand$ t\rightarrow t_{0}$.
Cette droite est alors la tangente à $ C$ en $ M_{0}$.
On parlera éventuellement de demi-tangente si on a une limite à droite ou une limite à gauche.

Voir la figure ci-dessous.

\includegraphics[

Comme il y a, selon son orientation, deux vecteurs unitaires qui dirigent une droite, cela revient à ce que le vecteur unitaire $ \pm\dfrac {\overrightarrow{M_{0}M}}{\left\Vert \overrightarrow{M_{0}M}\right\Vert }$ admet une limite quand $ M\rightarrow M_{0}$.
La tangente est alors la droite passant par $ M_{0}$ et dirigée par ce vecteur.

Définition :   Un point $ M_{0}\left( t_{0}\right) \in C$ est régulier$ \Leftrightarrow\overrightarrow{F^{\prime}\left( t_{0}\right) } \neq\overrightarrow{0}$.

Définition :   Un point non régulier est un point stationnaire.

Théorème :   En un point $ M_{0}\left( t_{0}\right) $ régulier, la courbe $ C$ admet une tangente dirigée par $ \overrightarrow{F^{\prime}\left( t_{0}\right) }$.

Preuve. On fait la démonstration pour une courbe plane, c'est exactement la même pour une courbe paramétrée de l'espace. $ \dfrac {\overrightarrow{M_{0}M}}{\left\Vert \overrightarrow{M_{0}M}\right\Vert }$ a pour coordonnées :

\begin{displaymath} \dfrac{1}{\left\Vert \overrightarrow{M_{0}M}\right\Vert }\l... ...right) -y\left( t_{0}\right) }{t-t_{0}} \end{array} \right) \end{displaymath}

Or

$\displaystyle \dfrac{t-t_{0}}{\left\Vert \overrightarrow{M_{0}M}\right\Vert }$

$\displaystyle =\dfrac {t-t_{0}}{\sqrt{\left( x\left( t\right) -x\left( t_{0}\right) \right) ^{2}+\left( y\left( t\right) -y\left( t_{0}\right) \right) ^{2}}}$

   

 

$\displaystyle =\dfrac{\pm1}{\sqrt{\left( \dfrac{x\left( t\right) -x\left( t_{0... ...+\left( \dfrac{y\left( t\right) -y\left( t_{0}\right) }{t-t_{0}}\right) ^{2}}}$

   

$\displaystyle \lim_{t\rightarrow t_{0}}\dfrac{t-t_{0}}{\left\Vert \overrightarrow{M_{0} M}\right\Vert }$

$\displaystyle =\dfrac{\pm1}{\sqrt{x^{\prime}\left( t_{0}\right) ^{2}+y^{\prime}\left( t_{0}\right) ^{2}}}$

   

$\displaystyle \lim_{t\rightarrow t_{0}}\dfrac{1}{\left\Vert \overrightarrow{M_{... ... t_{0}\right) \\ y\left( t\right) -y\left( t_{0}\right) \end{array} \right)$

$\displaystyle =\dfrac{\pm1}{\sqrt{x^{\prime}\left( t_{0}\right) ^{2}+y^{\prime... ...me}\left( t_{0}\right) \\ y^{\prime}\left( t_{0}\right) \end{array} \right)$

   


Ce qui assure le résultat. $ \qedsymbol$

Théorème :   $ M_{0}\left( t_{0}\right) $ un point stationnaire de $ C$, si$ \overrightarrow{F}$ est de classe suffisante au voisinage de $ t_{0}$, pour qu'il existe un vecteur dérivé non nul $ \overrightarrow{F^{\left( p\right) }\left( t_{0}\right) }$.
Alors, $ C$ admet en $ M_{0}$ une tangente ou des demi-tangentes.
Elles sont portées par ce premier vecteur dérivé non nul $ \overrightarrow{F^{\left( p\right) }\left( t_{0}\right) }$.
On note habituellement $ p$ l'ordre de dérivation de ce vecteur.

Preuve. On travaille ici exactement de la même façon dans le plan ou dans l'espace.
On fait un développement limité de $ \overrightarrow{F}$ à l'ordre $ p$, en tenant compte du fait que les dérivées aux ordres inférieurs à $ p$ sont nulles :

$\displaystyle \overrightarrow{M_{0}M}=\overrightarrow{F\left( t\right) }-\overr... ...\left( t-t_{0}\right) ^{p}\overrightarrow{\varepsilon\left( t-t_{0}\right) } $

Ce qui permet d'avoir le résultat annoncé en calculant la limite de$ \dfrac {\overrightarrow{M_{0}M}}{\left\Vert \overrightarrow{M_{0}M}\right\Vert }$. $ \qedsymbol$

1.2 Etude locale d'une courbe plane paramétrée

On appelle encore $ p$ le rang de dérivation du premier vecteur dérivé non nul, $ \overrightarrow{F^{\left( p\right) }\left( t_{0}\right) }\neq\overrightarrow{0}$, et $ q$ le rang du premier vecteur dérivé non colinéaire à $ \overrightarrow{F^{\left( p\right) }\left( t_{0}\right) }$, sous réserve bien sûr que $ \overrightarrow{F}$ soit de classe suffisante. $ \left( \overrightarrow{F^{\left( p\right) }\left( t_{0}\right) },\overrightarrow{F^{\left( q\right) }\left( t_{0}\right) }\right) $ est ainsi une famille libre.

Définition :   On dit que $ M_{0}$ est birégulier \begin{displaymath}\Leftrightarrow\left\{ \begin{array}[c]{c} p=1\\ q=2 \end{array} \right. \end{displaymath}

Dans tous les cas, on obtient l'allure locale de la courbe en faisant un développement limité à l'ordre $ q$ de $ \overrightarrow{F}$.

$\displaystyle \overrightarrow{M_{0}M}=\overrightarrow{F\left( t\right) }-\overr... ...\left( t-t_{0}\right) ^{q}\overrightarrow{\varepsilon\left( t-t_{0}\right) } $

Dans la base $ \left( \overrightarrow{F^{\left( p\right) }\left( t_{0}\right) },\overrightarrow{F^{\left( q\right) }\left( t_{0}\right) }\right) $, les coordonnées de $ \overrightarrow{M_{0}M}$ sont équivalentes à $ \dfrac{\left( t-t_{0}\right) ^{p}}{p!}$ et$ \dfrac{\left( t-t_{0}\right) ^{q}}{q!}$ quand $ t\rightarrow t_{0}$.
On travaille donc dans le repère $ \left( M_{0},\overrightarrow{F^{\left( p\right) }\left( t_{0}\right) },\overrightarrow{F^{\left( q\right) }\left( t_{0}\right) }\right) $, tout se décide alors suivant la parité de $ p$ et $ q$.
La courbe est toujours tangente à $ \overrightarrow{F^{\left( p\right) }\left( t_{0}\right) }$, la parité de $ p$ donne le signe de la coordonnée lorsque $ t<t_{0}$, la parité de $ q$ donne dans ce cas le signe de la deuxième coordonnée.
Dans les figures suivantes, le repère tracé est : $ \left( M_{0},\overrightarrow{F^{\left( p\right) }\left( t_{0}\right) },\overrightarrow{F^{\left( q\right) }\left( t_{0}\right) }\right) $.
On peut voir sur la figure ci-dessous l'ensemble des cas.

$\textstyle \parbox{3in}{\begin{center} \includegraphics[ width=3in ] {Etude... ...mpair} \textbf{et} $q$\ \textbf{pair} \textbf{: point ordinaire} \end{center}}$         $\textstyle \parbox{3in}{\begin{center} \includegraphics[ width=3in ]{Etude-l... ...} \textbf{et} $q$\ \textbf{impair} \textbf{: point d'inflexion} \end{center}}$$\textstyle \parbox{3in}{\begin{center} \includegraphics[ width=3in ] {Etude... ...broussement de }$\mathbf{1}^{\grave{e}re}$\ \textbf{esp\\lq {e}ce} \end{center}}$         $\textstyle \parbox{3in}{\begin{center} \includegraphics[ width=3in ] {Etude... ...broussement de }$\mathbf{2}^{\grave{e}me}$\ \textbf{esp\\lq {e}ce} \end{center}}$

Remarque :   En un point birégulier, la concavité est tournée vers$ \overrightarrow{F^{\prime\prime}\left( t_{0}\right) }$.

Remarque : 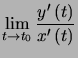  $ \lim\limits_{t\rightarrow t_{0}}\dfrac{y^{\prime}\left( t\right) }{x^{\prime}\left( t\right) }$     quand elle existe, est toujours la pente de la tangente à la courbe au point considéré.

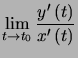Remarque :   Quand la pente de la tangente, donnée par $ \overrightarrow{F^{\left( p\right) }\left( t_{0}\right) }$ ou par $ \lim\limits_{t\rightarrow t_{0}}\dfrac{y^{\prime}\left( t\right) }{x^{\prime}\left( t\right) }$ est nulle ou infinie, c'est à dire quand la tangente horizontale ou verticale, la recherche de $ q$ est inutile puisque les variations de $ x\left( t\right) $ et $ y\left( t\right) $ permettent alors de déterminer le type de point.

Remarque :   Un point d'inflexion géométrique vérifie toujours \begin{displaymath}\left\vert \begin{array}[c]{ll} x^{\prime} & x^{\prime\prime}\\ y^{\prime} & y^{\prime\prime} \end{array} \right\vert =0\end{displaymath}.
A la demande de l'énoncé, on recherchera les point d'inflexion parmi ceux qui ont cette propriété.

Exemple :   On va faire l'étude locale de l'arc paramétré \begin{displaymath}:\left\{ \begin{array}[c]{l} x\left( t\right) =2t+t^{2}\\ y\left( t\right) =2t-\dfrac{1}{t^{2}} \end{array} \right. \end{displaymath} en $ t=-1.$ On a \begin{displaymath}:\left\{ \begin{array}[c]{l} x^{\prime}\left( t\right) =2+2... ...rime}\left( t\right) =2+\dfrac{2}{t^{3}} \end{array} \right. \end{displaymath} ce qui donne \begin{displaymath}:\left\{ \begin{array}[c]{l} x\left( -1\right) =-1\\ y\left( -1\right) =-3 \end{array} \right. \end{displaymath} et \begin{displaymath}:\left\{ \begin{array}[c]{l} x^{\prime}\left( -1\right) =0\\ y^{\prime}\left( -1\right) =0 \end{array} \right. ,\end{displaymath}

De plus \begin{displaymath}:\left\{ \begin{array}[c]{l} x^{\prime\prime}\left( t\right... ...prime}\left( t\right) =-\dfrac{6}{t^{4}} \end{array} \right. \end{displaymath} ce qui donne \begin{displaymath}:\left\{ \begin{array}[c]{l} x^{\prime\prime}\left( -1\righ... ... y^{\prime\prime}\left( -1\right) =-6 \end{array} \right. .\end{displaymath}

Enfin, \begin{displaymath}:\left\{ \begin{array}[c]{l} x^{\prime\prime\prime}\left( t... ...prime}\left( t\right) =\dfrac{24}{t^{5}} \end{array} \right. \end{displaymath} ce qui donne \begin{displaymath}:\left\{ \begin{array}[c]{l} x^{\prime\prime\prime}\left( -... ...prime\prime\prime}\left( -1\right) =-24 \end{array} \right. .\end{displaymath}

1.3 Branches infinies d'une courbe plane paramétrée

On dit que $ C$ admet une branche infinie quand $ x\left( t\right) $ ou$ y\left( t\right) $ tendent vers $ \pm\infty$ en $ t_{0}$ ou $ \pm\infty$.
Une hyperbole a ainsi 4 branches infinies.

  1. $ x(t)$ et $ y(t)\rightarrow\pm\infty$ quand $ t\rightarrow t_{0}$ on calcule $ \lim\limits_{t\rightarrow t_{0}}\dfrac{y(t)}{x(t)}$ appelée $ a$ si elle existe,
    1. si il n'y a pas de limite, on ne dit rien de plus.

      $ a=\pm\infty\quad$on a une branche parabolique de direction $ Oy$.

    2. $ a=0\quad$on a une branche parabolique de direction $ Ox$.
    3. dans les autres cas, on calcule $ \lim\limits_{t\rightarrow t_{0} }y(t)-ax(t)$ appelée $ b$,
      • si il n'y a pas de limite, on a une branche infinie de direction asymptotique $ y=ax$.

        $ b=\pm\infty\quad$on a une branche parabolique de direction $ y=ax$.

      • dans les autres cas, on a une asymptote $ y=ax+b$, de plus :
        • si $ y\left( t\right) -ax\left( t\right) -b>0$, la courbe est au dessus de l'asymptote,
        • si $ y\left( t\right) -ax\left( t\right) -b<0$, la courbe est au dessous de l'asymptote.

Exemple :   On va faire l'étude locale de l'arc paramétré \begin{displaymath}:\left\{ \begin{array}[c]{l} x\left( t\right) =t^{2}+\dfrac{2}{t}\\ y\left( t\right) =t+\dfrac{1}{t} \end{array} \right. \end{displaymath} en $ t=0^{+}.$$ x\left( t\right) $ et $ y\left( t\right) $ tendent tous deux vers$ +\infty$ en $ 0^{+},$ on a une branche infinie.$ \dfrac{y\left( t\right) }{x\left( t\right) }=\dfrac{t+\dfrac{1}{t}} {t^{2}+\dfrac{2}{t}}=\dfrac{t^{2}+1}{t^{3}+2}\underset{0}{\rightarrow} \dfrac{1}{2},$ et donc $ y=\dfrac{1}{2}x$ est direction asymptotique.$ y\left( t\right) -\dfrac{1}{2}x\left( t\right) =t-\dfrac{1}{2} t^{2}\underset{0^{+}}{\rightarrow}0^{+},$ et donc la droite $ y=\dfrac{1}{2}x$ est asymptote à la courbe en $ t=0^{+}$.
La courbe est donc au dessus de son asymptote.

Exemple :   On va faire l'étude locale de l'arc paramétré \begin{displaymath}:\left\{ \begin{array}[c]{l} x\left( t\right) =2t+t^{2}\\ y\left( t\right) =2t-\dfrac{1}{t^{2}} \end{array} \right. \end{displaymath} quand $ t\rightarrow+\infty.$$ x\left( t\right) $ et $ y\left( t\right) $ tendent tous deux vers$ +\infty$ en $ +\infty,$ on a une branche infinie.$ \dfrac{y\left( t\right) }{x\left( t\right) }=\dfrac{2t-\dfrac{1}{t^{2}} }{2t+t^{2}}=\dfrac{2t^{3}-1}{2t^{3}+t^{4}}\underset{+\infty}{\rightarrow}0.$
Quand $ t\rightarrow+\infty,$ on a une branche parabolique de direction $ Ox.$


© Christophe Caignaert - Lycée Colbert - Tourcoing