Chapitre 15 : Courbes

2 Courbes planes définies de façon implicite, Lignes de niveau

Sous-sections

2 Courbes planes définies de façon implicite, Lignes de niveau

2.1 Lignes de niveau

Définition :   $ F:\mathbb{R}^{2}\rightarrow\mathbb{R}$ de classe $ \mathcal{C}^{1}$ sur$ \mathcal{U}$ un ouvert de $ \mathbb{R}^{2}$. La courbe $ C$ d'équation$ F\left( x,y\right) =\lambda$ est l'ensemble des points de $ \mathcal{U}$ dont les coordonnées vérifient cette équation. C'est la ligne de niveau de $ F$ de hauteur $ \lambda$.

Définition :   Soit $ M_{0}\left( x_{0},y_{0}\right) $, un point de $ C$ d'équation$ F\left( x,y\right) =\lambda$.

$\displaystyle M_{0\text{ }}\text{est \textbf{singulier }}\Leftrightarrow\overrightarrow {Grad_{F}\left( M_{0}\right) }=\overrightarrow{0} $

2.2 Tangente en un point non singulier

Théorème :   Soit $ M_{0}\left( x_{0},y_{0}\right) $, un point de $ C$ d'équation$ F\left( x,y\right) =\lambda$, $ M_{0}$ non singulier. Alors $ C$ admet une tangente en $ M_{0}$, normale à $ \overrightarrow {Grad_{F}\left( M_{0}\right) }$.
Elle est donc d'équation :

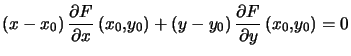
$\displaystyle \left( x-x_{0}\right) \dfrac{\partial F}{\partial x}\left( x_{0}... ...t( y-y_{0}\right) \dfrac{\partial F}{\partial y}\left( x_{0},y_{0}\right) =0 $

En un point singulier, il est possible que $ C$ ait une tangente comme il est possible qu'elle n'en ait pas.

Preuve. On admet que $ C$ puisse être paramétrée par $ t$ de telle façon que $ M_{0}$ soit un point régulier correspondant à $ t_{0}$.
Alors $ \forall t\in I,\quad f\left( t\right) =F\left( x\left( t\right) ,y\left( t\right) \right) =\lambda$, et $ f$ est de classe $ \mathcal{C}^{1}$.
On dérive, $ f^{\prime}\left( t_{0}\right) =0$ entraine

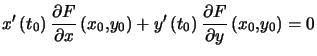
$\displaystyle x^{\prime}\left( t_{0}\right) \dfrac{\partial F}{\partial x}\left... ...eft( t_{0}\right) \dfrac{\partial F}{\partial y}\left( x_{0},y_{0}\right) =0 $

Ce qui prouve que le gradient est normal à la tangente. $ \qedsymbol$

Exemple :   On va chercher l'équation de la tangente au point $ \left( 1,1\right) $ à l'ellipse d'équation $ 4x^{2}+y^{2}=5.$
En $ \left( 1,1\right) ,$ le gradient est $ \left( 8,2\right) ,$ un vecteur normal à la courbe est donc : $ \left( 4,1\right)$.
La tangente a donc une équation de la forme     $ 4x+y=k$,     et comme elle passe par $ \left( 1,1\right) $, la tangente est d'équation :    $ 4x+y=5.$

2.3 Paramétrer une ligne de niveau

Comme il est plus facile de tracer une courbe paramétrée qu'une ligne de niveau, on cherche souvent à paramétrer celles ci.
Les deux moyens habituels sont :

  1. Poser : $ y=tx$, résoudre : $ f(x,tx)=0$ en $ x$, et on a alors la courbe paramétrée par $ t$.
  2. Passer en polaire et résoudre : $ f(\rho\cos\theta,\rho\sin\theta)=0$ en $ \rho$. On a alors la courbe de façon usuelle en polaires.


© Christophe Caignaert - Lycée Colbert - Tourcoing