Chapitre 15 : Courbes

3 Courbes planes en polaires

Sous-sections

3 Courbes planes en polaires

3.1 Courbes en coordonnées polaires

Définition : la courbe définie en coordonnées polaires par $\rho=f(\theta )=\rho(\theta)$ , $\theta\in I$ , est l'ensemble des points dont les coordonnées vérifient $\begin{displaymath}\left\{ \begin{array}[c]{l} x=\rho(\theta)\cos\theta\\ y=\rho(\theta)\sin\theta \end{array} \right. \end{displaymath}$ avec $\theta\in I$ .

On prendra toujours l'application $\rho$ au moins de classe $\mathcal{C}^{1}$ sur .

Remarque : Contrairement à ce qui se passe quand on prend des coordonnées polaires dans les intégrales doubles, cylindriques ou sphériques dans les intégrales triples, on admet ici que $\rho$ puisse être négatif.

La figure ci-dessous, montre un exemple de $\rho$ négatif.

$\includegraphics[$

3.2 Ensemble d'étude

En général, $\rho$ est -périodique. On cherche l'ensemble de définition, la périodicité, un premier ensemble d'étude : celui-ci doit être un multiple de la période et de $2\pi$ .
On recherche d'éventuelles symétries pour réduire l'ensemble d'étude.
On regarde en fait comment change $\rho$ quand on change $\theta$ , ce qui est résumé dans le tableau suivant :

$\theta$	$\rho$	admet
$\theta$ en $-\theta$	$\rho$ en $\rho$	une symétrie /
$\theta$ en $-\theta$	$\rho$ en $-\rho$	une symétrie /
$\theta$ en $\pi-\theta$	$\rho$ en $\rho$	une symétrie /
$\theta$ en $\pi-\theta$	$\rho$ en $-\rho$	une symétrie /
$\theta$ en $\pi+\theta$	$\rho$ en $\rho$	une symétrie / 0
$\theta$ en $\pi+\theta$	$\rho$ en $-\rho$	uniquement des points doubles

Dans chaque cas, on peut réduire l'intervalle d'étude.

3.3 Tangente

Théorème : la courbe définie en coordonnées polaires par $\rho=\rho(\theta)$ avec $\rho$ de classe $\mathcal{C}^{1}$ au voisinage de $\theta_{0}$ .
Alors admet une tangente en $M_{0}\left( \theta_{0}\right)$ définie par

$\displaystyle \tan V=\dfrac{\rho}{\rho^{\prime}}$

avec l'angle, orienté, entre le rayon vecteur et la tangente. En un point où $\rho(\theta_{0})=0$ , la tangente à la courbe est la droite $\theta=\theta_{0}$ .

Corollaire : Si de plus, $\rho\left( \theta_{0}\right) =0$ , alors

Conclusion : Dans tous les cas, l'équation de la tangente dans le repère local $\left( M_{0},\overrightarrow{u_{r}},\overrightarrow{u_{\theta} }\right)$ est : $Y=\tan V\ X$

Ceci est illustré par la figure déjà vue auparavent et la figure ci-dessous.

$\includegraphics[$

Preuve. On utilise ici les notations des physiciens $\overrightarrow{u_{r}}$ et $\overrightarrow{u_{\theta}}$ .

$\displaystyle \overrightarrow{OM}=\rho\left( \theta\right) \overrightarrow{u_{r}}$

et donc comme la dérivée de $\overrightarrow{u_{r}}$ par rapport à $\theta$ est $\overrightarrow{u_{\theta}}$

$\displaystyle \dfrac{\overrightarrow{dM}}{d\theta}=\rho^{\prime}\left( \theta\r... ... \overrightarrow{u_{r}}+\rho\left( \theta\right) \overrightarrow{u_{\theta}}$

En écrivant cette égalité en $\theta_{0}$ , on obtient que $\tan V=\dfrac{\rho\left( \theta_{0}\right) }{\rho^{\prime}\left( \theta _{0}\right) }$ , avec l'angle, orienté, entre le rayon vecteur et la tangente.
Si $\rho\left( \theta_{0}\right) =0$ , la pente de $\overrightarrow{M_{0} M}=\overrightarrow{OM}$ est $\dfrac{y}{x}=\dfrac{\rho\left( \theta\right) \sin\theta}{\rho\left( \theta\right) \cos\theta}$ qui tend bien vers $\tan \theta_{0}$ $\qedsymbol$

3.4 Branches infinies

On a une branche infinie quand $\lim\limits_{\theta\rightarrow\theta_{0}} \rho(\theta)$ est infini. On remarque que $\begin{displaymath}\left\{ \begin{array}[c]{c} \rho(\theta)\cos\left( \theta-\... ...a)\sin\left( \theta-\theta_{0}\right) =Y \end{array} \right. \end{displaymath}$ dans le repère tourné de $\theta_{0}$ .
Dans tous les cas, quand $\theta\rightarrow\theta_{0}$ $\begin{displaymath}\left\{ \begin{array}[c]{c} X\rightarrow\infty\\ \dfrac{Y}{X}\rightarrow0 \end{array} \right. \end{displaymath}$ La direction asymptotiques est donc toujours . Pour l'étude des branches infinies, on cherche donc : $\lim\limits_{\theta\rightarrow\theta_{0}}Y= \lim\limits_{\theta\rightarrow\theta_{0}}\rho(\theta)\sin\left( \theta-\theta_{0}\right)$ .

s'il n'y a pas de limite, on a une branche infinie de direction asymptotique .
cette limite est infinie, on a une branche parabolique de direction.
cette limite est finie $Y_{0}$ , on a une asymptote d'équation $Y=Y_{0}$ . Comme $X\sim\rho$ , on sait de quel coté de l'asymptote on est, puisqu'on a pris soin de tracer le repère local.

Ceci est illustré par la figure ci-dessous, avec : $Y=\overline{OP}$

$\includegraphics[$

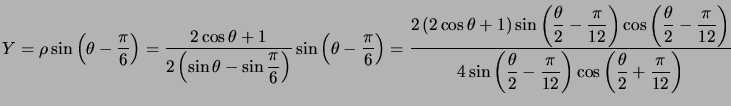
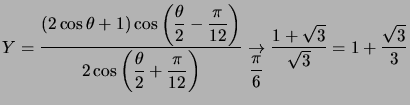
Exemple : On va étudier la branche infinie de la courbe d'équation $\rho =\dfrac{2\cos\theta+1}{2\sin\theta-1}$ en $\theta=\dfrac{\pi}{6}$ . $Y=\rho\sin\left( \theta-\dfrac{\pi}{6}\right) =\dfrac{2\cos\theta +1}{2\left(... ...-\dfrac{\pi} {12}\right) \cos\left( \dfrac{\theta}{2}+\dfrac{\pi}{12}\right) }$ $Y=\dfrac{\left( 2\cos\theta+1\right) \cos\left( \dfrac{\theta}{2} -\dfrac{\pi... ...dfrac{\pi}{6}}{\rightarrow}\dfrac{1+\sqrt{3}} {\sqrt{3}}=1+\dfrac{\sqrt{3}}{3}$
On a donc une asymptote d'équation $Y=1+\dfrac{\sqrt{3}}{3}$ dans le reprère tourné de $\dfrac{\pi}{6}$ par rapport à .

3.5 Plan d'étude

On a ici 2 originalités :

On ne fait l'étude des variations de $\rho$ par le signe de $\rho^{\prime}$ que si cette étude est simple ! On peut très bien s'en passer pour tracer la courbe !
Cependant, le calcul de $\rho^{\prime}$ reste nécessaire pour déterminer la tangente en des points particuliers.
Par contre, on fait l'étude indispensable du signe de $\rho$ , qui figure dans le tableau de « variations » et permet de déterminer dans quel cadran on trace la courbe.

On a donc :

Ensemble de définition, période, symétries, ensemble d'étude.
Tableau de « variations », $\theta$ , $\rho\left( \theta\right)$ , signe de $\rho$ , éventuellement $\rho^{\prime}$ , $\tan V=\dfrac{\rho} {\rho^{\prime}}$ .
Branches infinies.
Points essentiels et leurs tangentes.
Tracé de la courbe.

3.6 Exemple

On va étudier la courbe d'équation $\rho\left( \theta\right) =1-\cos\theta$ en coordonnées polaires. $\rho\left( \theta\right)$ est défine sur $\mathbb{R}$ , $2\pi$ périodique et paire.
On va donc étudier la fonction sur $\left[ 0,\pi\right]$ et il faudra compléter la courbe par une symétrie par rapport à .
On a $\rho^{\prime}=\sin\theta$ qui permet d'avoir le tableau de variation :
$\theta$
0

$\pi$
$\rho^{\prime}$
0
+
0
signe de $\rho$

+

$\rho$
0
$\nearrow$
2
$\tan V$
0

$\infty$

$\tan V=\dfrac{1-\cos\theta}{\sin\theta}=\tan\dfrac{\theta}{2}$ , on a facilement la tangente en $\theta=\pi,$ $\rho=2$ et $\tan V$ est infini et donc $V=\dfrac{\pi}{2}$ , en $\theta=\dfrac{\pi}{2}$ , $\rho=1$ et $\tan V=1$ et donc $V=\dfrac{\pi}{4}$ .
Il n'y a pas de branche infinie, il ne reste qu'à tracer la courbe.
Ceci est illustré par la figure ci-dessous.

$\includegraphics[$

3.7 Courbes usuelles en polaires

On a les coniques d'équation . est le paramètre de la conique, c'est à dire la distance du foyer à la directrice, et est l'excentricité de la conique.
- , correspond à une ellipse.
- , un parabole.
- , une hyperbole.
On montre ceci facilement en repassant en cartésiennes :
$\displaystyle \rho$
$\displaystyle =\dfrac{p}{1+e\cos\theta}$

$\displaystyle \rho+e\rho\cos\theta$
$\displaystyle =p$

$\displaystyle \rho$
$\displaystyle =p-ex$

$\displaystyle x^{2}+y^{2}$
$\displaystyle =\left( p-ex\right) ^{2}$

$\displaystyle \left( 1-e^{2}\right) x^{2}+y^{2}+2epx$
$\displaystyle =p^{2}$


qui est bien l'équation de la conique précisée selon les cas.
$\rho=\dfrac{d}{\cos\left( \theta-\theta_{0}\right) }\quad$ est une droite $\Delta$ , à la distance de , normale à la droite $\theta=\theta_{0}$ . On a dans le repère tourné de $\theta_{0}$
$\rho=A\cos\left( \theta-\theta_{0}\right) \quad$ est le cercle passant par de diamètre et de centre sur la droite $\theta=\theta_{0}$ .
Ce qui se montre facilement, on a ici, dans le repère tourné de $\theta_{0}$ :
$\displaystyle \rho^{2}$
$\displaystyle =A\rho\cos\left( \theta-\theta_{0}\right)$

$\displaystyle X^{2}+Y^{2}$
$\displaystyle =AX$

$\displaystyle \left( X-\frac{A}{2}\right) ^{2}+Y^{2}$
$\displaystyle =\frac{A^{2}}{4}$

$\theta$	0		$\pi$
$\rho^{\prime}$	0	+	0
signe de $\rho$		+
$\rho$	0	$\nearrow$	2
$\tan V$	0		$\infty$

$\displaystyle \rho$	$\displaystyle =\dfrac{p}{1+e\cos\theta}$
$\displaystyle \rho+e\rho\cos\theta$	$\displaystyle =p$
$\displaystyle \rho$	$\displaystyle =p-ex$
$\displaystyle x^{2}+y^{2}$	$\displaystyle =\left( p-ex\right) ^{2}$
$\displaystyle \left( 1-e^{2}\right) x^{2}+y^{2}+2epx$	$\displaystyle =p^{2}$

$\displaystyle \rho^{2}$	$\displaystyle =A\rho\cos\left( \theta-\theta_{0}\right)$
$\displaystyle X^{2}+Y^{2}$	$\displaystyle =AX$
$\displaystyle \left( X-\frac{A}{2}\right) ^{2}+Y^{2}$	$\displaystyle =\frac{A^{2}}{4}$