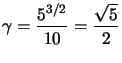Chapitre 15 : Courbes

4 Etude métrique des courbes planes paramétrées

Sous-sections

4 Etude métrique des courbes planes paramétrées

4.1 Longueur d'un arc, abscisse curviligne

Ce paragraphe est appliquable aux courbes paramétrées de l'espace.

Définition : Soit un arc paramétré du plan, ou de l'espace, tel que : $M\left( t\right)$ a pour coodonnées $\begin{displaymath}\left( \begin{array}[c]{c} x\left( t\right) \\ y\left( t\right) \end{array} \right) \end{displaymath}$ ou $\begin{displaymath}\left( \begin{array}[c]{c} x\left( t\right) \\ y\left( t\right) \\ z\left( t\right) \end{array} \right) \end{displaymath}$ avec , , de classe $\mathcal{C}^{1}$ sur un intervalle de $\mathbb{R}$ .
La longueur de entre $M\left( a\right)$ et $M\left( b\right)$ est selon les cas :

$\displaystyle L\left( C\right)$	$\displaystyle =\int_{a}^{b}\left\Vert \overrightarrow{M^{\prime}\left( t\right... ...a}^{b}\sqrt{x^{\prime}\left( t\right) ^{2}+y^{\prime}\left( t\right) ^{2}}\,dt$
$\displaystyle L\left( C\right)$	$\displaystyle =\int_{a}^{b}\left\Vert \overrightarrow{M^{\prime}\left( t\right... ...right) ^{2}+y^{\prime}\left( t\right) ^{2}+z^{\prime}\left( t\right) ^{2}}\,dt$

Théorème : Dans le cas d'une courbe plane définié en coordonnées polaires, la longueur de entre $M\left( \theta_{0}\right)$ et $M\left( \theta _{1}\right)$ est :

$\displaystyle L\left( C\right) =\int_{\theta_{0}}^{\theta_{1}}\left\Vert \overr... ...ho\left( \theta\right) ^{2}+\rho^{\prime}\left( \theta\right) ^{2}}\,d\theta$

Preuve. On a vu que $\overrightarrow{M^{\prime}\left( \theta\right) }=\rho^{\prime }\left( \theta\... ...\overrightarrow{u_{r}}+\rho\left( \theta\right) \: \overrightarrow{u_{\theta}}$ ce qui fournit immédiatement sa norme. $\qedsymbol$

Définition : un arc paramétré du plan ou de l'espace, de classe $\mathcal{C}^{1}$ sur .
On appelle abscisse curviligne de dans le sens des $\left( \text{ou }\theta\right)$ croissants et d'origine $M\left( t_{0}\right)$ $\left( \text{ou }M\left( \theta_{0}\right) \right)$ , selon les cas :

$\displaystyle s\left( t\right)$	$\displaystyle =\int_{t_{0}}^{t}\left\Vert \overrightarrow{M^{\prime }\left( u\right) }\right\Vert du$
$\displaystyle s\left( \theta\right)$	$\displaystyle =\int_{\theta_{0}}^{\theta}\left\Vert \overrightarrow{M^{\prime}\left( \varphi\right) }\right\Vert d\varphi$

On a alors

$\displaystyle \dfrac{ds}{dt}=\left\Vert \overrightarrow{M^{\prime}\left( t\right) }\right\Vert$ ou $\displaystyle \dfrac{ds}{d\theta}=\left\Vert \overrightarrow{M^{\prime}\left( \theta\right) }\right\Vert$

ou encore, toujours selon les cas :

$\displaystyle ds$	$\displaystyle =\sqrt{x^{\prime2}(t)+y^{\prime2}(t)}\,dt=\sqrt{x^{\prime2} (t)+y^{\prime2}(t)+z^{\prime2}\left( t\right) }\,dt$
$\displaystyle ds$	$\displaystyle =\sqrt{\rho^{2}+\rho^{\prime2}}\,d\theta$

4.2 Repère de Frenet

Définition : un arc paramétré du plan, de classe $\mathcal{C}^{1}$ sur . $M_{t_{0}}$ un point régulier de . $\left( M_{t_{0}},\overrightarrow{T},\overrightarrow{N}\right)$ est lerepère de Frenet au point $M_{t_{0}}$ avec

$\displaystyle \overrightarrow{T}$	$\displaystyle =\dfrac{d\overrightarrow{OM}}{ds}=\dfrac{\dfrac { d\overrightarrow{OM}}{dt}}{\left\Vert \dfrac{ d\overrightarrow{OM}}{dt}\right\Vert }$ calculé au point considéré
	et $\displaystyle \left( \overrightarrow{T},\overrightarrow{N}\right)$ orthonormal direct.

$\includegraphics[$

Définition : Quand est paramétré par une abscisse curviligne, on dit que le paramétrage est normal.

Théorème : un arc paramétré du plan, de classe $\mathcal{C}^{2}$ sur . Alors $\dfrac{\overrightarrow{dT}}{ds}$ est colinéaire à $\overrightarrow{N}$ .

Preuve. On a $\overrightarrow{T}\cdot\overrightarrow{T}=1$ , d'où, en dérivant, $2\overrightarrow{T}\cdot\dfrac{\overrightarrow{dT}}{ds}=0$ , ce qui entraine $\dfrac{\overrightarrow{dT}}{ds}$ normal à $\overrightarrow{T}$ , donc colinéaire à $\overrightarrow{N}$ . $\qedsymbol$

Remarque : On a ici une différence avec les conventions des physiciens.
Pour nous, $\left( \overrightarrow{T},\overrightarrow{N}\right)$ est toujours direct, tandis que pour les physiciens, $\overrightarrow{N}$ dépend de la concavité, c'est à dire du fait qu'on tourne sur la gauche ou sur la droite.
Il est ainsi toujours tourné vers l'intérieur de la courbe.

4.3 Courbure d'une courbe plane, rayon de courbure, centre de Courbure, cercle osculateur

Définition : Le rayon de courbure , la courbure $\gamma$ en un point sont donnés par

$\displaystyle \dfrac{d\overrightarrow{T}}{ds}=\gamma\overrightarrow{N}=\dfrac{1} {R}\overrightarrow{N}$

C'est la première formule de Frenet.

Définition : Le centre de courbure $\Omega$ est

$\displaystyle \Omega=M+R$ $\displaystyle \overrightarrow{N}$

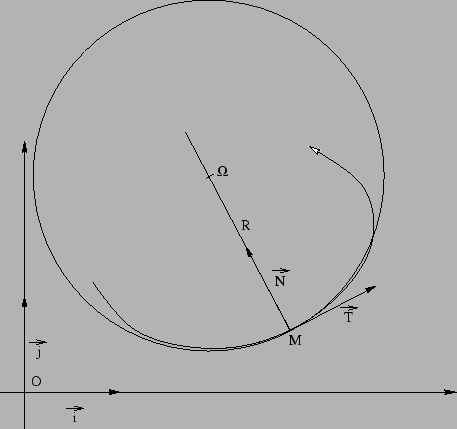
Le cercle de courbure ou cercle osculateur est le cercle de centre $\Omega$ et de rayon .
C'est le cercle le « mieux » tangent à la courbe au point .

On regardera avec soin la figure ci-dessous.

$\includegraphics[$

Théorème : On a aussi

$\displaystyle \dfrac{d\overrightarrow{N}}{ds}=-\gamma\overrightarrow{T}=-\dfrac{1} {R}\overrightarrow{T}$

C'est la deuxième formule de Frenet.

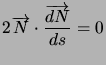Preuve. $\overrightarrow{N}\cdot\overrightarrow{N}=1$ , qu'on dérive $2\overrightarrow{N}\cdot\dfrac{\overrightarrow{dN}}{ds}=0$ . D'où $\dfrac{\overrightarrow{dN}}{ds}$ est colinéaire à $\overrightarrow{T}$ . De plus, $\overrightarrow{N}\cdot\overrightarrow{T}=0$ , qu'on dérive aussi, $\dfrac{\overrightarrow{dN}}{ds}\cdot\overrightarrow{T}+\overrightarrow {N}\cdot\dfrac{d\overrightarrow{T}}{ds}=0$ .
Mais $\overrightarrow{N} \cdot\dfrac{d\overrightarrow{T}}{ds}=\gamma$ . On a donc $\dfrac{\overrightarrow{dN}}{ds}\cdot\overrightarrow{T}=-\gamma$ et enfin $\dfrac{d\overrightarrow{N}}{ds}=-\gamma\overrightarrow{T}$ . $\qedsymbol$

Remarque : Si , on tourne à gauche et si , on tourne à droite. (la convention est différente de celle des physiciens pour lesquels est le rayon de courbure géométrique c'est à dire qu'on a toujours)

4.4 Calcul élémentaire de la courbure en un point birégulier

On considère la fonction anglaire associée $\varphi$ qui est l'angle entre et $\overrightarrow{T}$ , $\varphi=\widehat{\left( \overrightarrow{i},\overrightarrow{T}\right) }$ d'où, en paramétriques :

$\begin{displaymath}$

En polaires, on a :

$\displaystyle \varphi=\theta+V$

Théorème : Avec les notations précédentes, on a

$\displaystyle \gamma=\dfrac{d\varphi}{ds}\quad R=\dfrac{ds}{d\varphi}$

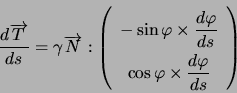Preuve. $\begin{displaymath}\overrightarrow{T}:\left( \begin{array}[c]{c} \cos\varphi\\ \sin\varphi \end{array} \right) \end{displaymath}$ qu'on dérive par rapport à . D'où $\begin{displaymath}\dfrac {d\overrightarrow{T}}{ds}=\gamma\overrightarrow{N}:\l... ... \cos\varphi\times\dfrac{ d\varphi}{ds} \end{array} \right) \end{displaymath}$ .
Ce qui donne immédiatement $\gamma=\dfrac{d\varphi}{ds}$ . $\qedsymbol$

4.5 Calcul pratique de la courbure en utilisant la fonction angulaire associée $\varphi$

On remarque que dans tous les cas, on a besoin de $\dfrac{ds}{dt}$ ou de $\dfrac{ds}{d\theta}$ .

En paramétriques, on peut parfois « reconnaître » directement la fonction $\varphi(t)$ en écrivant $\overrightarrow{T}$ .
Si on ne reconnait pas cette fonction, on écrit, à partir de $\overrightarrow{T}:$
$\displaystyle \tan\varphi=\dfrac{y^{\prime}}{x^{\prime}}$
Expression que l'on simplifie avant de dériver $\$ :
$\displaystyle \left( 1+\tan^{2}\varphi\right) \dfrac{d\varphi}{dt}$
$\displaystyle =\left( \dfrac{y^{\prime}}{x^{\prime}}\right) ^{\prime}$

$\displaystyle \dfrac{d\varphi}{dt}$
$\displaystyle =\dfrac{\left( \dfrac{y^{\prime}}{x^{\prime} }\right) ^{\prime}}{\left( 1+\tan^{2}\varphi\right) }$

Alors, on calcule facilement
$\displaystyle R=\dfrac{ds}{d\varphi}=\dfrac{ds}{dt}/\dfrac{d\varphi}{dt}$
En polaires :
$\displaystyle \varphi$
$\displaystyle =\theta+V$ avec $\displaystyle \tan V=\dfrac{\rho}{\rho^{\prime}},$ endérivant après simplification,

$\displaystyle \dfrac{d\varphi}{d\theta}$
$\displaystyle =1+\dfrac{dV}{d\theta}$

Ce qui permet de calculer :
$\displaystyle R=\dfrac{ds}{d\varphi}=\dfrac{ds}{d\theta}/\dfrac{d\varphi}{d\theta}$

Exemple : On va chercher le rayon de courbure en tous points de la courbe de représentation paramétrique : $\begin{displaymath}\left\{ \begin{array}[c]{l} x=\left( 1+\cos^{2}t\right) \sin t\\ y=\sin^{2}t\cos t \end{array} \right. \end{displaymath}$ .
On obtient facilement $\begin{displaymath}:\left\{ \begin{array}[c]{l} x^{\prime}=\left( 3\cos^{2}t-1... ...\prime}=\sin t\left( 3\cos^{2}t-1\right) \end{array} \right. \end{displaymath}$ d'où $\dfrac{ds}{dt}=\left\vert 3\cos^{2}t-1\right\vert$ et $\tan\varphi=\tan t,$ ce qui donne $\dfrac{d\varphi}{dt}=1$ .
Enfin, $R=\dfrac{ds}{d\varphi}=\left\vert 3\cos^{2}t-1\right\vert$
On peut continuer le calcul et on obtient : $\overrightarrow{T}=$ signe $(3\cos ^2t-1) \left( \begin{array}[c]{c} \cos t\\ \sin t \end{array} \right)$ , puis : $\overrightarrow{N}=$ signe $(3\cos ^2t-1) \left( \begin{array}[c]{c} -\sin t\\ \cos t \end{array} \right)$ .
Les coordonnées du centre de courbure sont donc : $\begin{displaymath}\left\{ \begin{array}[c]{l} x=2\sin^{3}t\\ y=2\cos^{3}t \end{array} \right. \end{displaymath}$ .

Exemple : On va chercher le rayon de courbure en tous points de la courbe d'équation $\rho=1-\cos\theta$ en coordonnées polaires.
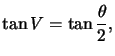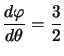On a déjà calculé $\tan V=\tan\dfrac{\theta}{2},$ et ainsi $\dfrac{dV}{d\theta}=\dfrac{1}{2},$ puis $\dfrac{d\varphi}{d\theta}=\dfrac {3}{2}$ . $\rho^{2}+\rho^{\prime2}=2\left( 1-\cos\theta\right)$ qui donne $\dfrac {ds}{d\theta}=\sqrt{2\left( 1-\cos\theta\right) }$ .
Enfin, $R=\dfrac{ds}{d\varphi}=\dfrac{2\sqrt{2\left( 1-\cos\theta\right) } }{3}$ .

4.6 Calcul direct des éléments de courbure

On peut aussi rechercher, si on aime les calculs, des formules directes donnant courbure et rayon de courbure.

Si $\dfrac{y^{\prime}}{x^{\prime}}$ ou $\dfrac{\rho}{\rho^{\prime}}$ ne se simplifient pas du tout, les calculs sont les mêmes que ceux faits en utilisant la fonction angulaire associée,
mais, si $\dfrac{y^{\prime}}{x^{\prime}}$ ou $\dfrac{\rho}{\rho^{\prime}}$ se simplifient, ne serait-ce qu'un peu, les calculs seront plus longs, et souvent plus complexes, en utilisant le calcul direct qu'en utilisant la fonction angulaire associée.

C'est pourquoi, on réserve cette méthode quand on travaille pour une valeur particulière du paramètre.

Dans le cas $\begin{displaymath}\left\{ \begin{array}[c]{l} x=f(t)=x(t)\\ y=g(t)=y(t) \end{array} \right. \end{displaymath}$
$\begin{displaymath}$
$\begin{displaymath} R=\dfrac{\left( x^{\prime2}+y^{\prime2}\right) ^{\frac{3}{2... ...\ y^{\prime} & y^{\prime\prime} \end{array} \right\vert } \end{displaymath}$
$\begin{displaymath} \Omega :\left\{ \begin{array}[c]{l} X=x-y^{\prime}\dfrac{... ...rime\prime} \end{array} \right\vert } \end{array} \right. \end{displaymath}$
Dans le cas , on considère qu'on a une courbe paramétrée par $\begin{displaymath}\left\{ \begin{array}[c]{l} x=x\\ y=f(x) \end{array} .\right. \end{displaymath}$
Ceci évite d'avoir à mémoriser de nouvelles formules...
Dans le cas des coordonnées polaires $\rho=\rho(\theta):$
$\displaystyle R=\dfrac{\left( \rho^{2}+\rho^{\prime2}\right) ^{\frac{3}{2}}}{\rho^{2}+2\rho^{\prime2}-\rho\rho^{\prime\prime}}$

Preuve. Il nous faut démontrer ces dernières formules, en particulier :     $\begin{displaymath} R=\dfrac{\left( x^{\prime2}+y^{\prime2}\right) ^{\frac{3}{2... ...\ y^{\prime} & y^{\prime\prime} \end{array} \right\vert } \end{displaymath}$      et :     $R=\dfrac{\left( \rho^{2}+\rho^{\prime2}\right) ^{\frac{3}{2}}}{\rho^{2}+2\rho^{\prime2}-\rho\rho^{\prime\prime}}$ .
En paramétriques, on a :     $\left( 1+\tan^{2}\varphi\right) \dfrac{d\varphi}{dt}=\left( \dfrac {y^{\prime}}{x^{\prime}}\right) ^{\prime}$ et $R=\dfrac{ds}{d\varphi }=\dfrac{\frac{ds}{dt}}{\frac{d\varphi}{dt}}$      donne :     $R=\dfrac{\sqrt{x^{\prime2}+y^{\prime2}}}{\dfrac{\dfrac{y^{\prime\prime }x^{\p... ...ght) ^{\frac{3}{2} }}{y^{\prime\prime}x^{\prime}-y^{\prime}x^{\prime\prime}}$
En polaires, $\tan V=\dfrac{\rho} {\rho^{\prime}}$ donne :     $\dfrac{dV}{d\theta}=\dfrac{\dfrac{\rho^{\prime2}-\rho\rho^{\prime\prime}} {\r... ...}}}=\dfrac{\rho^{\prime 2}-\rho\rho^{\prime\prime}}{\rho^{2}+\rho^{\prime2}}$      et donc :     $\dfrac{d\varphi}{d\theta}=1+\dfrac{dV}{d\theta}=\dfrac{\rho^{2}+2\rho ^{\prime2}-\rho\rho^{\prime\prime}}{\rho^{2}+\rho^{\prime2}}$
Et enfin,     $R=\dfrac{ds}{d\varphi}=\dfrac{\frac{ds}{d\theta}}{\frac{d\varphi}{d\theta} }=... ...2}\right) ^{\frac{3}{2}}}{\rho ^{2}+2\rho^{\prime2}-\rho\rho^{\prime\prime}}$ $\qedsymbol$

Remarque : Dans le cas d'une courbe définie en coordonnées polaire, lespoints d'inflexion vérifient

$\displaystyle \rho^{2}+2\rho^{\prime2}-\rho\rho^{\prime\prime}=0$

puisqu'en un point d'inflexion, la courbure est nulle.

4.7 Cas particulier de la valeur 0 du paramètre

Il s'agit ici du cas où on utilisera systématiquement les formules de calcul direct.

Enfin, dans le cas où on est en paramétriques et où $\Omega$ correspond à la valeur 0 du paramètre.
Un développement limité à l'ordre 2 de et en 0 fournit, par la formule de Taylor,
$\displaystyle x\left( t\right)$
$\displaystyle =x\left( 0\right) +x^{\prime}\left( 0\right) t+\dfrac{x^{\prime\prime}\left( 0\right) }{2}t^{2}+o\left( t^{2}\right)$

$\displaystyle y\left( t\right)$
$\displaystyle =y\left( 0\right) +y^{\prime}\left( 0\right) t+\dfrac{y^{\prime\prime}\left( 0\right) }{2}t^{2}+o\left( t^{2}\right)$

$x^{\prime}(0),x^{\prime\prime}(0),y^{\prime}(0),y^{\prime\prime}(0)$ qui permettent de calculer facilement .
On peut faire la même chose en polaires si on cherche la courbure à la valeur 0 de $\theta$ .
Un développement limité à l'ordre 2 de $\rho(\theta)$ en 0 fournit $\rho(0),\rho^{\prime}(0)$ , et $\rho^{\prime\prime}(0)$ .
$\displaystyle \rho\left( \theta\right) =\rho\left( 0\right) +\rho^{\prime}\left... ...\rho^{\prime\prime}\left( 0\right) }{2}\theta ^{2}+o\left( \theta^{2}\right)$

Exemple : On va chercher la courbure de la courbe d'équation polaire $\rho\left( \theta\right) =\dfrac{\cos\theta-2\sin\theta}{1+\sin^{3}\theta}$ au point $\left( 0,1\right)$ correspondant à la valeur 0 du paramètre. $\rho\left( \theta\right) =\dfrac{1-2\theta-\theta^{2}/2+o\left( \theta ^{2}\r... ...+o\left( \theta^{2}\right) }=1-2\theta-\theta^{2}/2+o\left( \theta^{2}\right)$ Ce qui nous donne $:\rho\left( 0\right) =1,$ $\rho^{\prime}\left( 0\right) =-2$ et $\rho^{\prime\prime}\left( 0\right) =-1$ et enfin $\gamma =\dfrac{5^{3/2}}{10}=\dfrac{\sqrt{5}}{2}$

$\displaystyle \left( 1+\tan^{2}\varphi\right) \dfrac{d\varphi}{dt}$	$\displaystyle =\left( \dfrac{y^{\prime}}{x^{\prime}}\right) ^{\prime}$
$\displaystyle \dfrac{d\varphi}{dt}$	$\displaystyle =\dfrac{\left( \dfrac{y^{\prime}}{x^{\prime} }\right) ^{\prime}}{\left( 1+\tan^{2}\varphi\right) }$

$\displaystyle \varphi$	$\displaystyle =\theta+V$ avec $\displaystyle \tan V=\dfrac{\rho}{\rho^{\prime}},$ endérivant après simplification,
$\displaystyle \dfrac{d\varphi}{d\theta}$	$\displaystyle =1+\dfrac{dV}{d\theta}$

$\displaystyle x\left( t\right)$	$\displaystyle =x\left( 0\right) +x^{\prime}\left( 0\right) t+\dfrac{x^{\prime\prime}\left( 0\right) }{2}t^{2}+o\left( t^{2}\right)$
$\displaystyle y\left( t\right)$	$\displaystyle =y\left( 0\right) +y^{\prime}\left( 0\right) t+\dfrac{y^{\prime\prime}\left( 0\right) }{2}t^{2}+o\left( t^{2}\right)$