Chapitre 16 : Surfaces

1 Nappes Paramétrées

Sous-sections


1 Nappes Paramétrées

1.1 Nappe paramétrée

Définition :   Soit $ \mathcal{D}$ un ouvert de $ \mathbb{R}^{2}$, et $ f:\mathcal{D} \rightarrow\mathbb{R}^{3}$, de classe $ \mathcal{C}^{1}.$$ \mathcal{S}=f\left( \mathcal{D}\right) $ est appelée nappe paramétrée par $ f.$
En pratique,

\begin{displaymath}

Si $ f$ est de classe $ \mathcal{C}^{k}$, on parle de nappe paramétrée de classe $ \mathcal{C}^{k}.$

Définition :   Soit $ \mathcal{S}=\left( \mathcal{D},f\right) $ une nappe paramétrée de classe $ \mathcal{C}^{k}$ $ \left( k\geqslant1\right) $,\begin{displaymath}M_{0}:\left( \begin{array}[c]{c} x\left( u_{0},v_{0}\right)... ...}\right) \\ z\left( u_{0},v_{0}\right) \end{array} \right) \end{displaymath} un point de la nappe.
On dit que $ M_{0}$ est régulier $ \Leftrightarrow\left( \dfrac{\overrightarrow{\partial M}}{\partial u}\left( u... ...rac{\overrightarrow{\partial M}}{\partial v}\left( u_{0},v_{0}\right) \right) $ forment une famille libre     \begin{displaymath}\Leftrightarrow\left( \left( \begin{array}[c]{c} \dfrac{\pa... ... \dfrac{\partial z}{\partial v} \end{array} \right) \right) \end{displaymath} forment une famille libre
$ \Leftrightarrow$ ces deux vecteurs ne sont pas colinéaires.

1.2 Plan tangent en un point régulier d'une nappe paramétrée

Théorème :   Soit $ \mathcal{S}=\left( \mathcal{D},f\right) $ une nappe paramétrée de classe $ \mathcal{C}^{k}$ $ \left( k\geqslant1\right) $,\begin{displaymath}M_{0}:\left( \begin{array}[c]{c} x\left( u_{0},v_{0}\right)... ...{array}[c]{c} x_{0}\\ y_{0}\\ z_{0} \end{array} \right) \end{displaymath} un point régulier, alors $ \mathcal{S}$ admet un plan tangent en $ M_{0}.$
C'est le plan $ \left( M_{0},\dfrac{\overrightarrow{\partial M}}{\partial u}\left( u_{0},v_{0... ...ac{\overrightarrow{\partial M}}{\partial v}\left( u_{0},v_{0}\right) \right) .$
Son équation est :

\begin{displaymath} \left\vert \begin{array}[c]{ccc} \left( X-x_{0}\right) & ... ...tial v}\left( u_{0},v_{0}\right) \end{array} \right\vert =0 \end{displaymath}

Le vecteur :    $ \dfrac{\overrightarrow{\partial M}}{\partial u}\left( u_{0},v_{0}\right) \wedge\dfrac{\overrightarrow{\partial M}}{\partial v}\left( u_{0} ,v_{0}\right) $     est normal à la surface au point.

Preuve.     $ \overrightarrow{M_{0}M}=\left( u-u_{0}\right) \dfrac{\overrightarrow {\partia... ...ial M}}{\partial v}\left( u_{0},v_{0}\right) +o\left( u-u_{0},v-v_{0}\right) $ ce qui prouve que     $ \lim\limits_{\left( u,v\right) \rightarrow\left( u_{0},v_{0}\right) }\dfrac{\overrightarrow{M_{0}M}}{\left\Vert \overrightarrow{M_{0}M}\right\Vert } $     est bien dans la direction du plan indiqué. $ \qedsymbol$

La figure ci-dessous montre le plan tangent et le vecteur normal à une surface.

\includegraphics[width=4.5558in]{Plan-Tangent}

Les courbes tracées sur la surface sont les courbes à $ u$ ou à $ v$ constants, il apparaît bien ici que le plan tangent est engendré par les tangentes à ces courbes au point considéré.

Exemple :   On va chercher, s'il existe, le plan tangent à la nappe \begin{displaymath}:\left\{ \begin{array}[c]{l} x=u+v\\ y=u-v\\ z=u^{2}-v^{2} \end{array} \right. \end{displaymath} au point \begin{displaymath}\left( \begin{array}[c]{l} 3\\ 1\\ 3 \end{array} \right) \end{displaymath} correspondant aux valeurs $ u=2$ et $ v=1$ des paramètres.
On calcule les dérivées partielles par rapprortà $ u$ puis leur valeur au point : \begin{displaymath}\left\{ \begin{array}[c]{l} \dfrac{\partial x}{\partial u}=... ...=1\\ \dfrac{\partial z}{\partial u}=2u \end{array} \right. \end{displaymath} qui au point indiqué est le vecteur \begin{displaymath}\left( \begin{array}[c]{c} 1\\ 1\\ 4 \end{array} \right) \end{displaymath}
On fait de même avec $ v$:\begin{displaymath}\left\{ \begin{array}[c]{l} \dfrac{\partial x}{\partial v}=... ...1\\ \dfrac{\partial z}{\partial v}=-2v \end{array} \right. \end{displaymath} qui au point indiqué est le vecteur \begin{displaymath}\left( \begin{array}[c]{c} 1\\ -1\\ -2 \end{array} \right) \end{displaymath}
Le plan tangent est donc, s'il existe, d'équation : \begin{displaymath}\left\vert \begin{array}[c]{ccc} x-3 & 1 & 1\\ y-1 & 1 & -1\\ z-3 & 4 & -2 \end{array} \right\vert =0\end{displaymath}, soit : $ 2x+6y-2z=6$.
Enfin, le plan tangent (qui existe !) est d'équation : $ x+3y-z=3$

1.3 Courbe tracée sur une nappe paramétrée

Elle peut correspondre à $ u$ ou $ v$ constant, ce sont par exemple les courbes que trace Maple quand il trace en « fil de fer » une nappe paramétrée.
D'une façon plus générale, une courbe tracée sur une nappe paramétrée correspond souvent à avoir l'un des paramètres en fonction de l'autre (via si possible une fonction de classe $ \mathcal{C}^{1} $). On obtient ainsi une courbe paramétrée de l'espace (de classe$ \mathcal{C}^{1} $).
La tangente à la courbe, quand elle existe est alors tracée sur le plan tangent. On montrera ceci dans un autre cadre.


1.4 Paramétrisation cartésienne

Définition :   On dit qu'on a une paramétrisation cartésienne quand on a $ x$ et $ y$ comme paramètres.
On note alors simplement

$\displaystyle z=f\left( x,y\right) $

$ \left( x,y\right) \in\mathcal{D}$, avec $ f$ de classe $ \mathcal{C}^{k}$.

Théorème :   Soit $ \mathcal{S}$ une nappe paramétrée cartésienne définie par $ z=f\left( x,y\right) $, $ \left( x,y\right) \in\mathcal{D}$, avec $ f$ de classe $ \mathcal{C}^{k}$, $ k\geqslant2$.
Soit \begin{displaymath}M_{0}:\left( \begin{array}[c]{c} x_{0}\\ y_{0}\\ z_{0} \end{array} \right) \end{displaymath} un point de $ \mathcal{S}$.
Soit

$\displaystyle r=\dfrac{\partial^{2}f}{\partial x^{2}}\left( x_{0},y_{0}\right) ... ...ght) ,\quad t=\dfrac{\partial^{2}f}{\partial y^{2}}\left( x_{0},y_{0}\right) $

Preuve. On applique la formule de Taylor-Toung à l'ordre 2, toutes les dérivées partielles étant prises en $ \left( x_{0},y_{0}\right) :$

$\displaystyle z-z_{0}$

$\displaystyle =f\left( x,y\right) -f\left( x_{0},y_{0}\right)$

   

 

$\displaystyle =\underbrace{\left( \left( x-x_{0}\right) \dfrac{\partial f}{\par... ...x}+\left( y-y_{0}\right) \dfrac{\partial f}{\partial y}\right) }_{=z_1-z_{0} }$

   

 

$\displaystyle +\underbrace{\dfrac{1}{2}\left( \left( x-x_{0}\right) ^{2}\dfrac{... ... \left( y-y_{0}\right) \end{array} \right) \right\Vert ^{2}\right)}_{=z-z_1}$

   


Le point $ M_1$ de coordonnées $ \left( x,y,z_1 \right)$ étant un point du plan tangent. Le signe de $ \left( z-z_{1}\right) $ permet de déterminer de quel coté du plan tangent est le point $ M$.
On a :

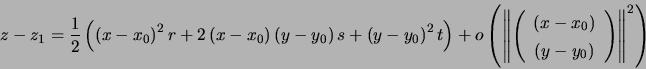
\begin{displaymath} z-z_{1}=\dfrac{1}{2}\left( \left( x-x_{0}\right) ^{2}r+2\le... ... y-y_{0}\right) \end{array} \right) \right\Vert ^{2}\right) \end{displaymath}

$ \left( z-z_{1}\right) $ finit par être du signe de l'expression du second degré quand elle n'est pas nulle.
On pose

$\displaystyle \Delta=4\left( s^{2}-rt\right) $

$ \qedsymbol$

Exemple :   On va chercher la nature du point \begin{displaymath}\left( \begin{array}[c]{c} 1\\ 1\\ 0 \end{array} \right) \end{displaymath} de la nappe paramétrée cartésienne d'équation :

$\displaystyle z=f\left( x,y\right) =x^{2}-y^{2}.$

Cette équation est clairement de classe $ \mathcal{C}^{2}$ au moins. On calcule les dérivées partielles premières et secondes.$ \dfrac{\partial f}{\partial x}=2x,\quad\dfrac{\partial f}{\partial y}=-2y,\qu... ...l^{2} f}{\partial x\partial y}=0,\quad\dfrac{\partial^{2}f}{\partial y^{2}}=-2$.
Au point considéré, (et d'ailleurs en tous points), $ r=2$, $ s=0$,$ t=-2$, $ s^{2}-rt=4>0$.
Le point \begin{displaymath}\left( \begin{array}[c]{c} 1\\ 1\\ 0 \end{array} \right) ,\end{displaymath} comme tous les points, est en col.


© Christophe Caignaert - Lycée Colbert - Tourcoing