Chapitre 16 : Surfaces

2 Surfaces définies par une Equation Cartésienne

Sous-sections


2 Surfaces définies par une Equation Cartésienne

2.1 Surface d'équation cartésienne $ F\left ( x,y,z\right ) =0$

Définition :   $ \mathcal{U}$ un ouvert de $ \mathbb{R}^{3}$, $ F:\mathcal{U}\rightarrow \mathbb{R}$ de classe $ \mathcal{C}^{k}$, $ k\geqslant1.$
$ \mathcal{S}$, la surface d'équation cartésienne $ F\left ( x,y,z\right ) =0$ est l'ensemble des points :    \begin{displaymath}    tels que :    $ F\left ( x,y,z\right ) =0$

Définition :   $ \mathcal{U}$ un ouvert de $ \mathbb{R}^{3}$, $ F:\mathcal{U}\rightarrow \mathbb{R}$ de classe $ \mathcal{C}^{k}$, $ k\geqslant1.$ $ \mathcal{S}$ d'équation cartésienne $ F\left ( x,y,z\right ) =0$,$ M_{0}$ est ditsingulier $ \Leftrightarrow\overrightarrow{Grad_{F}\left( M_{0}\right) }=\overrightarrow{0}$

On ne confondra pas les points singuliers d'une surface définie par une équation cartésienne et les points réguliers d'une nappe paramétrée...

2.2 Plan tangent à $ S$ en un point non singulier

Théorème :   $ \mathcal{U}$ un ouvert de $ \mathbb{R}^{3}$, $ F:\mathcal{U}\rightarrow \mathbb{R}$ de classe $ \mathcal{C}^{k}$, $ k\geqslant1$.$ \mathcal{S}$ d'équation cartésienne $ F\left ( x,y,z\right ) =0$,$ M_{0}$ un point non singulier de $ \mathcal{S}$.
Alors $ \mathcal{S}$ admet un plan tangent en $ M_{0}$.
Ce plan passe par$ M_{0}$ et est normal au vecteur $ \overrightarrow{Grad_{F}\left( M_{0}\right) }$.
Son équation est donc :     $ \overrightarrow{M_{0}M}\cdot\overrightarrow{Grad_{F}\left( M_{0}\right) }=0 $     ou encore :     \begin{displaymath} dF_{M_{0}}\left( \begin{array}[c]{c} x-x_{0}\\ y-y_{0}\\ z-z_{0} \end{array} \right) =0 \end{displaymath}     ou enfin :     $ \left( x-x_{0}\right) \dfrac{\partial F}{\partial x}\left( x_{0} ,y_{0},z_{0}... ..._{0}\right) \dfrac{\partial F}{\partial z}\left( x_{0},y_{0},z_{0}\right) =0 $

Remarque :   On a bien sûr la même figure que pour une nappe paramétrée. Seul le calcul du vecteur normal change.

Preuve. On admet que $ \mathcal{S}$ a aussi au voisinage de $ M_{0}$ une représentation paramétrique de classe $ \mathcal{C}^{1} $ $ \left( u,v\right) \rightarrow\overrightarrow{f\left( u,v\right) }$ sur $ \mathcal{D}$ un ouvert de $ \mathbb{R}^{2}$.$ M_{0}$ correspondant aux valeurs $ \left( u_{0},v_{0}\right) $ des paramètres.
On a donc :

$\displaystyle \forall\left( u,v\right) \in\mathcal{D},$ $\displaystyle F\left( \overrightarrow {f\left( u,v\right) }\right) =0=H\left( u,v\right) $

Sa différentielle en $ \left( u_{0},v_{0}\right) $ est aussi nulle,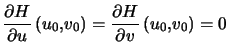$ \dfrac{\partial H}{\partial u}\left( u_{0},v_{0}\right) =\dfrac{\partial H}{\partial v}\left( u_{0},v_{0}\right) =0$, donc, en ne précisant pas en quels points on prend les dérivées, pour alléger les notations :

$\displaystyle \dfrac{\partial F}{\partial x}\times\dfrac{\partial x}{\partial u... ...partial u} +\dfrac{\partial F}{\partial z}\times\dfrac{\partial z}{\partial u}$

$\displaystyle =0$

   

$\displaystyle \dfrac{\partial F}{\partial x}\times\dfrac{\partial x}{\partial v... ...partial v} +\dfrac{\partial F}{\partial z}\times\dfrac{\partial z}{\partial v}$

$\displaystyle =0$

   


Egalités qu'on peut interpréter comme des produits scalaires :

$\displaystyle \overrightarrow{Grad_{F}\left( M_{0}\right) }\cdot\dfrac{\overrightarrow {\partial f}}{\partial u}\left( u_{0},v_{0}\right)$

$\displaystyle =0$

   

$\displaystyle \overrightarrow{Grad_{F}\left( M_{0}\right) }\cdot\dfrac{\overrightarrow {\partial f}}{\partial v}\left( u_{0},v_{0}\right)$

$\displaystyle =0$

   


Ce qui prouve que la direction du plan tangent à la nappe est le plan normal à $ \overrightarrow{Grad_{F}\left( M_{0}\right) }$. $ \qedsymbol$

Remarque :   $ z=f\left( x,y\right) $ a la particularité de pouvoir être considéré comme une nappe paramétrée par $ x$ et $ y$, ou comme une surface d'équation cartésienne $ z-f\left( x,y\right) =0$. Rechercher le plan tangent selon l'un ou l'autre des points de vue conduit à des calculs différents, mais au même résultat !

Exemple :   On reprend la nappe d'équation $ g\left( x,y,z\right) =z-x^{2}-y^{2}=0$, et on cherche le plan tangent en \begin{displaymath}\left( \begin{array}[c]{c} 1\\ 1\\ 0 \end{array} \right) \end{displaymath}.
Cette équation est clairement de classe $ \mathcal{C}^{1} $ au moins.
Au point considéré, $ \dfrac{\partial g}{\partial x}=-2$, $ \dfrac{\partial g}{\partial y}=2$ et $ \dfrac{\partial g}{\partial z}=1$.
Le plan tangent est donc d'équation $ -2\left( x-1\right) +2\left( y-1\right) +z=0$, ou encore $ 2x-2y-z=0$.

2.3 Tangente à une courbe paramétrée tracée sur une surface

Théorème :   $ \Gamma$ une courbe paramétrée de classe $ \mathcal{C}^{1} $ tracée sur $ \mathcal{S}$ de classe $ \mathcal{C}^{1} $.
En un point régulier de$ \Gamma$, et non singulier de $ \mathcal{S,}$ la tangente à $ \Gamma$ est tracée sur le plan tangent à $ \mathcal{S}$.

Preuve.\begin{displaymath}\Gamma:M:\left( \begin{array}[c]{c} x\left( t\right) \\ y\left( t\right) \\ z\left( t\right) \end{array} \right) \end{displaymath}, $ t\in I$, et $ \mathcal{S}:F\left( x,y,z\right) =0$, $ M_{0}$ correspondant à $ t_{0}$ et on a :

$\displaystyle \forall t\in I,$ $\displaystyle F\left( x\left( t\right) ,y\left( t\right) ,z\left( t\right) \right) =0 $

On différencie en $ t_{0}$, cela donne :     $ \dfrac{\partial F}{\partial x}\times x^{\prime}\left( t_{0}\right) +\dfrac{\p... ...ight) +\dfrac{\partial F}{\partial z}\times z^{\prime}\left( t_{0}\right) =0 $ On le réécrit :     $ \overrightarrow{Grad_{F}\left( M_{0}\right) }\cdot\dfrac{\overrightarrow {dM}}{dt}\left( t_{0}\right) =0 $
Ceci prouve que le vecteur tangent à $ \Gamma$ est dans la direction du plan tangent à $ \mathcal{S}$, et comme tous deux passent par $ M_{0}$, on a le résultat annoncé. $ \qedsymbol$

2.4 Tangente à une courbe intersection de surfaces cartésiennes

Théorème :   $ \mathcal{S}_{1}$ et $ \mathcal{S}_{2}$ deux surfaces de classe $ \mathcal{C}^{1} $ d'équations \begin{displaymath}\left\{ \begin{array}[c]{l} F_{1}\left( x,y,z\right) =0\\ F_{2}\left( x,y,z\right) =0 \end{array} \right. \end{displaymath}
Soit $ M_{0}$ un point non singulier de $ \mathcal{S}_{1}$ et$ \mathcal{S}_{2}$, tel que les plans tangents à $ \mathcal{S}_{1}$ et$ \mathcal{S}_{2}$ en $ M_{0}$ sont distincts.
Et enfin :     $ \Gamma=\mathcal{S}_{1}\cap\mathcal{S}_{2} $. Alors, la tangente à $ \Gamma$ en $ M_{0}$, si elle existe, est l'intersection des deux plans tangents.
Elle est dirigée par

$\displaystyle \overrightarrow{Grad_{F_{1}}\left( M_{0}\right) }\wedge\overrightarrow {Grad_{F_{2}}\left( M_{0}\right) } $

Preuve. Puisque la tangente, si elle existe, est tracée sur chacun des plans tangents... $ \qedsymbol$

2.5 Projection d'une courbe sur les plans de coordonnées

Une courbe dans l'espace peut toujours être définie par intersection de surfaces cartésiennes ou en paramétriques.
On va voir comment obtenir ces projections (orthogonales) dans chacun des cas.

2.6 Equation cartésienne d'une nappe paramétrée

On a la nappe paramétrée \begin{displaymath}\mathcal{S}:\left( u,v\right) \in\mathcal{D},\left\{ \begin... ...]{l} x=x(u,v)\\ y=y(u,v)\\ z=z(u,v) \end{array} \right. \end{displaymath}
On cherche l'équation cartésienne d'une surface$ \mathcal{S}^{\prime}$ qui contient $ \mathcal{S}.$
Cela revient à chercher une relation entre $ x,y,z$ qui ne contient ni $ u$ ni $ v$.
Pour cela, on élimine les 2 paramètres entre les 3 équations.
On élimine l'un des 2 paramètres puis l'autre.
Il faut prendre soin d'éviter les dénominateurs, qui nous obligeraient à considérer des cas particuliers inutilement.
On travaille à priori par implications.

Pour savoir si on a ajouté des points, il faut chercher si pour un point de la surface on peut retrouver les valeurs des paramètres qui corespondent à ce point.
C'est toujours une tâche un peu délicate, qu'on ne réalise qu'à la demande explicite de l'énoncé ...

Exemple :   On va chercher une équation cartésienne de la nappe paramétrée : \begin{displaymath}\left\{ \begin{array}[c]{l} x=u-v\\ y=uv\\ z=u^{2}+v^{2} \end{array} \right. \end{displaymath}.
On peut facilement éliminer $ u$ en utilisant la première équation : $ u=x+v$.
Ce qui donne : \begin{displaymath}\left\{ \begin{array}[c]{l} y=xv+v^{2}\\ z=x^{2}+2xv+2v^{2} \end{array} \right. \end{displaymath}, ou encore, en éliminant les termes en $ v^{2}$ de la seconde équation : \begin{displaymath}\left\{ \begin{array}[c]{l} y=xv+v^{2}\\ z-2y=x^{2} \end{array} \right. \end{displaymath}.
La dernière équation ne contient plus de paramètres... L'équation cherchée est $ x^{2}+2y-z=0$.
C'est l'équation d'une surface $ \mathcal{S}^{\prime}$ qui contient la nappe paramétrée.


© Christophe Caignaert - Lycée Colbert - Tourcoing