Chapitre 16 : Surfaces

3 Lignes de Plus Grande Pente

Sous-sections

3 Lignes de Plus Grande Pente

3.1 Ligne de plus grande pente

Définition : Les lignes de plus grand pente d'une surface sont les trajectoires orthogonales des lignes de niveau de cette surface.

3.2 Recherche des lignes de plus grande pente de $z=f\left( x,y\right)$

Les lignes de niveau vérifient $\lambda=f\left( x,y\right)$ . On paramètre ces courbes par , on obtient $\begin{displaymath}M\left( t,\lambda\right) :\left\{ \begin{array}[c]{l} x=x(t,\lambda)\\ y=y(t,\lambda)\\ z=\lambda \end{array} \right. \end{displaymath}$
On applique alors le chapitre précédent relatif aux trajectoires orthogonales.
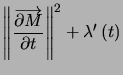
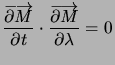
On rappelle que cela revient à résoudre : $\left\Vert \dfrac{\overrightarrow{\partial M}}{\partial t}\right\Vert ^{2} +\lambda^{\prime}\left( t\right)$ $\dfrac{\overrightarrow{\partial M} }{\partial t}\cdot\dfrac{\overrightarrow{\partial M}}{\partial\lambda}=0$

Exemple : On cherche, en liaison avec le chapitre précédent, les lignes de plus grande pente de la surface d'éqution .
Les lignes de niveau sont les hyperboles $xy=\lambda$ , $\lambda\in\mathbb{R}$ . comme on l'a déjà fait :
On paramètre ces hyperboles $\begin{displaymath}M:\left\{ \begin{array}[c]{c} x=t\\ y=\dfrac{\lambda}{t}... ... \begin{array}[c]{c} 0\\ \dfrac{1}{t} \end{array} \right. \end{displaymath}$
On cherche $\lambda$ sous la forme $\lambda\left( t\right)$

$\displaystyle \dfrac{\overrightarrow{\partial M}}{\partial t}\cdot\left( \dfrac... ...me}\left( t\right) \dfrac{\overrightarrow{\partial M}}{\partial\lambda}\right)$	$\displaystyle =\left( \begin{array}[c]{c} 1\\ -\dfrac{\lambda}{t^{2}} \end... ...) \left( \begin{array}[c]{c} 0\\ \dfrac{1}{t} \end{array} \right) \right)$
	$\displaystyle =1+\dfrac{\lambda^{2}}{t^{4}}-\dfrac{\lambda\lambda^{\prime}}{t^{3}}=0$

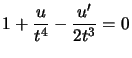On pose $u=\lambda^{2}$ , on obtient : $1+\dfrac{u}{t^{4}}-\dfrac{u^{\prime}}{2t^{3}}=0$ qui est linéaire du premier ordre.
On cherche la solution générale comme au chapitre précédent.
On obtient les courbes vérifiant : $\begin{displaymath}\left\{ \begin{array}[c]{l} z=xy\\ y^{2}-x^{2}=\mu \end{array} \right. \end{displaymath}$ .
Leurs projections orthogonales sur le plan horizontal forment un réseau d'hyperboles.