Chapitre 17 : Cylindres, Cônes et Surface de Révolution

1 Cylindres

Sous-sections

1 Cylindres

1.1 Cylindre

Définition : Un cylindre de direction $\overrightarrow{u}$ est une surface formée d'une famille de droites de direction $\overrightarrow{u}$ .
Ces droites sont les génératrices du cylindre. Une courbe qui rencontre toutes les génératrices est unedirectrice.
L'intersection de la surface avec un plan perpendiculaire à la direction $\overrightarrow{u}$ , est une section droite du cylindre.

La figure ci-dessous montre des exemples de « cylindres ».

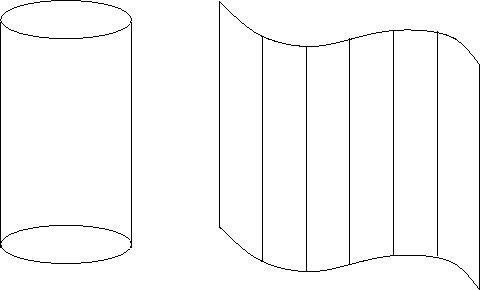
$\includegraphics[$

Remarque : Un cylindre n'est pas, en général, un cylindre de révolution !

Définition : Si $\mathcal{S}$ est une surface, l'ensemble des points de $\mathcal{S}$ tels que la direction du plan tangent à $\mathcal{S}$ en contient $\overrightarrow{u}$ est le contour apparent de $\mathcal{S}$ dans la direction $\overrightarrow{u}$ . Le cylindre de direction $\overrightarrow{u}$ et de directrice ce contour apparent est le cylindre circonscrit à $\mathcal{S}$ dans la direction $\overrightarrow{u}$ .

1.2 Equation d'un cylindre

Théorème : $\mathcal{S}$ est un cylindre de direction $\overrightarrow{k}\Leftrightarrow \mathcal{S}$ a une équation de la forme .
C'est aussi dans le plan l'équation de la section droite de $\mathcal{S}$ .

Remarque : La courbe d'équation dans le plan est la section droite du cylindre d'équation dans l'espace.
Ainsi, l'interprétation d'une équation incomplète (en , ou ou ) est celle d'une courbe ou d'une surface...

De même, s'il manque dans l'équation, on a un cylindre de direction $\overrightarrow{j}$ .

Preuve. On admet que $\mathcal{S}$ a une équation de la forme $H\left( x,y,z\right) =0$ . Mais, si $\begin{displaymath}M_{0}:\left( \begin{array}[c]{c} x_{0}\\ y_{0}\\ z_{0} \end{array} \right) \end{displaymath}$ appartient à $\mathcal{S}$ , la droite $\left( M_{0} ,\overrightarrow{k}\right)$ est tracée sur $\mathcal{S}$ et donc : $\quad \forall z\in\mathbb{R},H\left( x_{0},y_{0},z\right) =0$
Ce qui prouve qu'en fait, ne dépend pas de .
On peut donc écrire : $\quad H\left( x,y,z\right) =F(x,y)$ $\qedsymbol$

Théorème : $\mathcal{S}$ est un cylindre de direction $\overrightarrow{u}\Leftrightarrow\mathcal{S}$ a une équation de la forme

$\displaystyle F(P_{1},P_{2})=0$

avec $P_{1}\left( x,y,z\right) =k_{1}$ et $P_{2}\left( x,y,z\right) =k_{2}$ , l'équation de deux plans.
Et enfin, $P_{1}\cap P_{2}$ donne la direction $\overrightarrow{u}$ .

Preuve. Un changement de repère orthonormal où $\overrightarrow{K} //\overrightarrow{u}$ , fournit $F\left( X,Y\right) =0$ , et en revenant dans le repère d'origine, $F(P_{1},P_{2})=0$ . $\qedsymbol$

1.3 Plan tangent le long d'une génératrice

Théorème : Le plan tangent à un cylindre le long d'un génératrice est invariant.

Preuve. Quitte à changer de repère, on peut travailler avec .
Le plan tangent le long de la génératrice $\left( x_{0},y_{0} ,\lambda\right)$ est d'équation :

$\displaystyle \left( x-x_{0}\right) \dfrac{\partial F}{\partial x}\left( x_{0}... ...t( y-y_{0}\right) \dfrac{\partial F}{\partial y}\left( x_{0},y_{0}\right) =0$

qui clairement ne contient pas $\lambda$ . $\qedsymbol$

1.4 Equation d'un cylindre de direction et de directrice données

On va chercher l'équation d'un cylindre $\Sigma$ de direction $\overrightarrow{u}$ et de directrice $\Gamma$ donnés.

Faire une figure symbolique, comme la figure ci-dessous.

$\includegraphics[$

Partir d'un point quelconque du cylindre $\Sigma$ cherché $\begin{displaymath}M:\left( \begin{array}[c]{l} X\\ Y\\ Z \end{array} \right) \end{displaymath}$
Ecrire que la droite (décrite en paramétrique) rencontre
Pour cela, on a, en pratique, deux cas selon que est donnée en paramétriques ou par intersection de surfaces.
- Si $\Gamma$ est définie en paramétriques. On a $\begin{displaymath}\overrightarrow{u}:\left( \begin{array}[c]{c} \alpha\\ \beta\\ \gamma \end{array} \right) \end{displaymath}$ , et $\begin{displaymath}\Gamma:\left\{ \begin{array}[c]{c} x\left( t\right) \\ y\left( t\right) \\ z\left( t\right) \end{array} \right. t\in I\end{displaymath}$
  $\begin{displaymath} M:\left( \begin{array}[c]{l} X\\ Y\\ Z \end{array} ... ...a\\ z\left( t\right) =Z+\lambda\gamma \end{array} \right. \end{displaymath}$
  On a directement une représentation de $\Sigma$ en nappe paramé trée.
  Pour obtenir une équation cartésienne, on élimine $\lambda$ et entre ces deux équations, on obtient l'équation d'un cylindre $\Sigma^{\prime}$ qui contient le cylindre cherché.
- Si $\Gamma$ est définie par intersection de surfaces. On a $\begin{displaymath}\overrightarrow{u}:\left( \begin{array}[c]{c} \alpha\\ \beta\\ \gamma \end{array} \right) \end{displaymath}$ , et $\begin{displaymath}\Gamma:\left\{ \begin{array}[c]{c} F\left( x,y,z\right) =0\\ G\left( x,y,z\right) =0 \end{array} \right. \end{displaymath}$
  $\begin{displaymath} M:\left( \begin{array}[c]{l} X\\ Y\\ Z \end{array} ... ...+\lambda\beta,Z+\lambda\gamma\right) =0 \end{array} \right. \end{displaymath}$
  On élimine le paramètre $\lambda$ , on obtient l'équation d'un cylindre $\Sigma^{\prime}$ qui contient $\Sigma$ le cylindre cherché.

Remarque : Dans le cas où $\Gamma$ est définie en paramétriques $\begin{displaymath}\Gamma:\left\{ \begin{array}[c]{c} x\left( t\right) \\ y\left( t\right) \\ z\left( t\right) \end{array} \right. t\in I\end{displaymath}$ , on peut aussi paramétrer la droite de direction $\begin{displaymath}\overrightarrow{u}:\left( \begin{array}[c]{c} \alpha\\ \beta\\ \gamma \end{array} \right) \end{displaymath}$ passant par un point de $\Gamma$ , on obtient : $\begin{displaymath}M:\left( \begin{array}[c]{l} X\\ Y\\ Z \end{array} \r... ...ta\\ Z=z\left( t\right) +\lambda\gamma \end{array} \right. \end{displaymath}$
Par rapport à la méthode précédente, cela revient à changer $\lambda$ et $-\lambda$ . On a encore directement une représentation en nappe paramétrée.

Exemple : On cherche une équation cartésienne du cylindre $\Sigma$ de direction $\begin{displaymath}\overrightarrow{u}:\left( \begin{array}[c]{l} 1\\ 1\\ 0 \end{array} \right) \end{displaymath}$ et de directrice définie par $\begin{displaymath}t\in\mathbb{R}:\left\{ \begin{array}[c]{l} x=\cos t\\ y=\sin t\\ z=t \end{array} \right. \end{displaymath}$ .
On a donc $\begin{displaymath}M:\left( \begin{array}[c]{l} X\\ Y\\ Z \end{array} \r... ...t=X+\lambda\\ \sin t=Y+\lambda\\ t=Z \end{array} \right. \end{displaymath}$ .
On élimine facilement , ce qui donne $\begin{displaymath}\left\{ \begin{array}[c]{l} \cos Z=X+\lambda\\ \sin Z=Y+\lambda \end{array} \right. \end{displaymath}$ .
Tout aussi facilement, on élimine $\lambda$ , et on obtient enfin : $\cos Z-\sin Z=X-Y$ qui est l'équation d'un cylindre $\Sigma^{\prime}$ qui contient le cylindre cherché.

1.5 Recherche du contour apparent

On cherche le contour apparent de la surface $\mathcal{S}$ d'équation dans la direction $\begin{displaymath}\overrightarrow{u}:\left( \begin{array}[c]{c} \alpha\\ \beta\\ \gamma \end{array} \right) \end{displaymath}$ .
Pour cela, on prend un point de la surface $\mathcal{S}$ , et on écrit que le gradient de en ce point est normal à $\overrightarrow{u}$ .
Cela donne :

$\displaystyle F\left( x,y,z\right)$	$\displaystyle =0$
$\displaystyle \alpha\dfrac{\partial F}{\partial x}\left( x,y,z\right) +\beta \... ...z}\left( x,y,z\right) +\gamma\dfrac{\partial F}{\partial z}\left( x,y,z\right)$	$\displaystyle =0$

On a le ainsi contour apparent par intersection de surfaces.

1.6 Equation d'un cylindre circonscrit à une surface

Il suffit de chercher le contour apparent, puis de chercher le cylindre de la direction donnée et de directrice ce contour apparent.

Exemple : On cherche une équation cartésienne du cylindre $\Sigma$ de direction $\begin{displaymath}\overrightarrow{u}:\left( \begin{array}[c]{l} 1\\ 1\\ 0 \end{array} \right) \end{displaymath}$ circonscrit à $\mathcal{S}$ d'équation : $x^{2}+y^{2}-z=0$ .
Le contour apparent est donné comme on vient de le voir par : $\begin{displaymath}\left\{ \begin{array}[c]{l} x ^{2}+ y ^{2}-z=0\\ 2 x +2 y =0 \end{array} \right. \end{displaymath}$ . On a donc $\begin{displaymath}M:\left( \begin{array}[c]{l} X\\ Y\\ Z \end{array} \r... ...mbda\right) +2\left( Y+\lambda\right) =0 \end{array} \right. \end{displaymath}$ .
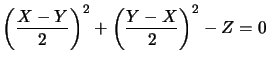On élimine $\lambda$ en réécrivant la deuxième équation, $\lambda=-\dfrac{X+Y}{2}$ , et on obtient : $\left( \dfrac{X-Y}{2}\right) ^{2}+\left( \dfrac{Y-X}{2}\right) ^{2}-Z=0$ ou encore $\left( X-Y\right) ^{2}-2Z=0$ qui est l'équation d'un cylindre $\Sigma^{\prime}$ qui contient le cylindre cherché.