Définition : ![]() une droite de l'espace. Un cercle de l'espace est d'axe
une droite de l'espace. Un cercle de l'espace est d'axe ![\begin{displaymath}\Delta\Leftrightarrow\left\{ \begin{array}[c]{l} \text{son ... ...e} dans un plan orthogonal \\lq {a} }\Delta \end{array} \right. \end{displaymath}](img114.png)
Définition : Une surface de révolution d'axe ![]() est formée d'une famille de cercles d'axe
est formée d'une famille de cercles d'axe ![]() Un plan contenant l'axe de révolution est un plan méridien, son intersection avec la surface est une méridienne.
Un plan contenant l'axe de révolution est un plan méridien, son intersection avec la surface est une méridienne.
La méridienne est symétrique par rapport à l'axe de ré volution. On parle donc parfois de demi-méridienne.
Une surface de révolution est donc engendrée par la rotation d'une méridienne ou d'une demi-méridienne autour de l'axe de révolution.
Théorème : Une surface est de révolution d'axe ![]() elle a une équation de la forme
elle a une équation de la forme
![]()
Preuve.![]() est un plan méridien. La méridienne est symétrique par rapport à
est un plan méridien. La méridienne est symétrique par rapport à ![]() . Elle est donc d'équation
. Elle est donc d'équation ![]() .
.
L'équation en coordonnées cylindriques est donc ![]() .
.
On obtient donc en coordonnées cartésiennes ![]() .
. ![]()
Théorème : Une surface de révolution ![]() d'axe
d'axe ![]() a une équation de la forme :
a une équation de la forme : ![]() avec
avec ![\begin{displaymath} \left\{ \begin{array}[c]{l} S\left( x,y,z\right) =R^{2}\q... ...=k\quad\text{l'\'{e}quation d'un plan.} \end{array} \right. \end{displaymath}](img122.png)
L'axe de révolution ![]() est orthogonal à
est orthogonal à ![]() et passe par le centre de
et passe par le centre de ![]() .
.
Preuve. Dans un repère orthonormal centré sur ![]() , tel que
, tel que![]() est dans la direction de
est dans la direction de ![]() ,
, ![]() a une équation de la forme :
a une équation de la forme : ![]()
Ou encore : ![]() Or, en utilisant le produit scalaire et la norme :
Or, en utilisant le produit scalaire et la norme : ![]()
On obtient : ![]() et
et ![]()
Ce qui donne le résultat. ![]()
Il s'agit de rechercher l'équation d'une surface de révolution d'axe![]() dont on connait une demi-méridienne ou une méridienne.
dont on connait une demi-méridienne ou une méridienne.
Si on a une demi-méridienne dans le plan ![]() , elle est d'équation :
, elle est d'équation : ![]()
En complétant par symétrie, la méridienne complète est d'équation : ![]()
Ce qu'on réécrit : ![]()
Alors la surface de révolution est simplement d'équation : ![]()
Pour cela, on utilise simplement les coordonnées cylindriques.
Exemple : On va chercher l'équation du tore de révolution engendré par la rotation du cercle du plan ![]() d'équation
d'équation ![]() autour de
autour de ![]() .
.
Ce cercle est une demi-méridienne, l'autre demi-méridienne est d'équation ![]() , et donc la méridienne :
, et donc la méridienne :![]() .
.
Ce qu'on réécrit : ![]() .
.
Il suffit alors de remplacer ![]() par
par ![]() et on obtient :
et on obtient : ![]() .
.
On recherche ici l'équation d'une surface de révolution ![]() engendrée par la rotation de
engendrée par la rotation de ![]() autour de
autour de ![]() . on traite ici le cas général.
. on traite ici le cas général.
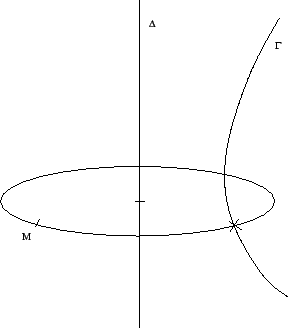
![\begin{displaymath}M:\left( \begin{array}[c]{l} X\\ Y\\ Z \end{array} \right) \end{displaymath}](img39.png)
Pour cela, on a en pratique deux cas selon que ![]() est donné en paramétriques ou par intersection de surfaces.
est donné en paramétriques ou par intersection de surfaces.
![\begin{displaymath}\Omega:\left( \begin{array}[c]{c} a\\ b\\ c \end{array} \right) \end{displaymath}](img87.png) et
et ![\begin{displaymath}\overrightarrow{u}:\left( \begin{array}[c]{c} \alpha\\ \beta\\ \gamma \end{array} \right) \end{displaymath}](img43.png) et enfin
et enfin ![\begin{displaymath}\Gamma:\left\{ \begin{array}[c]{c} x\left( t\right) \\ y\left( t\right) \\ z\left( t\right) \end{array} \right. \end{displaymath}](img75.png)
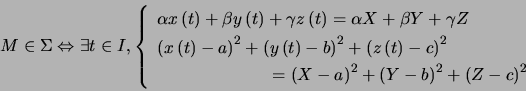
![\begin{displaymath}\Omega:\left( \begin{array}[c]{c} a\\ b\\ c \end{array} \right) \end{displaymath}](img87.png) et
et ![\begin{displaymath}\overrightarrow{u}:\left( \begin{array}[c]{c} \alpha\\ \beta\\ \gamma \end{array} \right) \end{displaymath}](img43.png) et enfin
et enfin ![\begin{displaymath}\Gamma:\left\{ \begin{array}[c]{c} F\left( x,y,z\right) =0\\ G\left( x,y,z\right) =0 \end{array} \right. \end{displaymath}](img48.png)
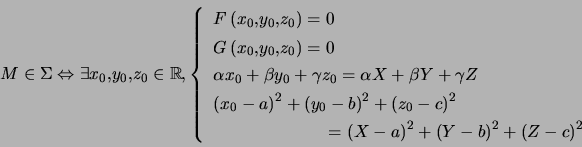
Exemple : On va chercher l'équation de la surface de révolution ![]() engendrée par la rotation de la courbe
engendrée par la rotation de la courbe ![\begin{displaymath}\Gamma:\left\{ \begin{array}[c]{l} x=t\\ y=t^{2}\\ z=1+t \end{array} \right. \end{displaymath}](img146.png) autour de l'axe
autour de l'axe ![]() passant par
passant par ![]() et de vecteur directeur
et de vecteur directeur![]() .
.
Soit ![\begin{displaymath}M:\left( \begin{array}[c]{c} X\\ Y\\ Z \end{array} \right) \end{displaymath}](img148.png) appartenant à la surface, Le cercle d'axe
appartenant à la surface, Le cercle d'axe ![]() passant par
passant par![]() , le plan passant par
, le plan passant par ![]() et perpendiculaire à
et perpendiculaire à ![]() , et
, et ![]() ont un point commun.
ont un point commun.
Ce qui donne, compte tenu qu'on remplace le cercle par la sphère de centre ![]() passant par
passant par ![\begin{displaymath}M:\exists t\in\mathbb{R}:\left\{ \begin{array}[c]{l} t^{2}+... ...) ^{2}=X^{2}+Y^{2}+Z^{2}\\ t+t^{2}=X+Y \end{array} \right. \end{displaymath}](img149.png) .
.
On sort ![]() de la seconde équation, on le plonge dans la première, ce qui donne :
de la seconde équation, on le plonge dans la première, ce qui donne : ![]() puis
puis ![]() .
.
On a ainsi : ![\begin{displaymath}\left\{ \begin{array}[c]{l} 2t\left( X+Y\right) =1+2\left( ... ...^{2}+Y^{2}+Z^{2}\right) \\ t+t^{2}=X+Y \end{array} \right. \end{displaymath}](img153.png) .
.
On multiplie la deuxième par ![]() et on remplace en utilisant la première :
et on remplace en utilisant la première :
![]() .
.
On obtient l'équation d'une surface qui contient la surface de révolution cherchée.