Chapitre 17 : Cylindres, Cônes et Surface de Révolution
Remarque : On ne cherche pas l'équation d'un cylindre ou d'un cône de révolution comme celle d'un cylindre ou d'un cône ni comme celle d'une surface de révolution !...
- Pour un cylindre de révolution défini par son axe
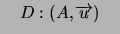 et son rayon
et son rayon 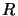
On cherche l'ensemble des points  tels que la distance de
tels que la distance de  à
à 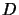 vaut
vaut 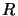 :
: 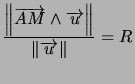
En pratique, on élève tout au carré pour avoir une égalité équivalente sans racines carrées. - Pour un cône de révolution défini par son axe
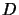 dirigé par
dirigé par  , son sommet
, son sommet  et son demi angle au sommet
et son demi angle au sommet 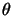
On cherche l'ensemble des points  tels que l'angle
tels que l'angle  a pour mesure
a pour mesure 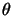 en tant qu'angle non orienté de droites :
en tant qu'angle non orienté de droites : 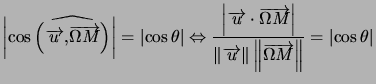
En pratique, on élève tout au carré pour éviter les valeurs absolues et les racines carrées.
© Christophe Caignaert - Lycée Colbert - Tourcoing
 a pour mesure
a pour mesure