Chapitre 18 : Quadriques

1 Etude des quadriques

Sous-sections

1 Etude des quadriques

1.1 Quadriques propres ou dégénérées

Définition : Une quadrique est une surface dont l'équation est un polynôme du second degré en $x,\; y,\; z$ .

Les quadriques sont en quelque sorte à l'espace ce que les coniques sont au plan.
Certaines quadriques sont dites dégénérées.
Ainsi, une « quadrique » peut être :

vide, par exemple $:x^{2}+y^{2}+z^{2}=-1$
un point, par exemple $:x^{2}+y^{2}+z^{2}=0$
une droite, par exemple $:x^{2}+y^{2}=0$
un plan, par exemple $:x^{2}=0$
deux plans, par exemple ou $x^{2}-y^{2}=0$ ou $x^{2}=1$

D'autres quadriques ne sont que des cas particuliers de surfaces déjà étudiées, ce sont :

des cylindres à base :
- elliptique, dont certains de révolution, par exemple : $x^{2} +y^{2}=1$ ou $x^{2}+2y^{2}=1$
- parabolique, par exemple : $y=x^{2}$ , ou
- hyperbolique, par exemple : $x^{2}-y^{2}=1$
des cônes, dont certains de révolution, par exemple : $x^{2}+y^{2}-z^{2}=0$ .

Les autres quadriques sont les quadriques dites propres, objet réel de ce chapitre.

1.2 Intersection avec un plan

Théorème : L'intersection d'une quadrique (dégénérée ou non) avec un plan est une conique (dégénérée ou non).

Remarque : Attention , l'intersection d'une quadrique propre avec un plan peut être une conique dégénérée...

Preuve. Un changement de repère, orthonormal ou non, transforme une équation du second degré en une équation du second degré.
On peut donc supposer que le plan est d'équation $\mathcal{P}:z=0$ .

$\displaystyle \mathcal{Q}:ax^{2}+by^{2}+cz^{2}+2dxy+2exz+2fyz+gx+hy+iz+j=0$

a pour intersection avec $\mathcal{P}$ :

$\displaystyle \mathcal{C}:ax^{2}+by^{2}+2dxy+gx+hy+j=0$

On a bien l'équation générale d'une conique. $\qedsymbol$

L'intersection d'une quadrique avec un plan étant une conique, l'intersection d'une quadrique de révolution d'axe $\Delta$ avec un plan méridien est une conique dont $\Delta$ est axe de symétrie... Une quadrique de révolution est donc engendrée par la rotation d'une conique autour d'un de ses axes de symétrie.
Certaines quadriques quadriques ainsi obtenues sont des cylindres et des cônes de révolution.
Mais certaines quadriques sont de « nouvelles » surfaces, quadriques dites propres.
On va ainsi trouver :

Le paraboloïde de révolution, obtenu en faisant tourner une parabole autour de son axe.
L'ellipsoïde de révolution, obtenu en faisant tourner une ellipse autour d'un de ses axes. Il sera en forme de « ballon de rugby » si l'axe de révolution est l'axe focal de l'ellipse et en forme de « soucoupe » si l'axe de révolution est l'axe non focal de l'ellipse.
L'hyperboloïde de révolution à une nappe, obtenu en faisant tourner une hyperbole autour de son axe non focal.
L'hyperboloïde de révolution à deux nappes, obtenu en faisant tourner une hyperbole autour de son axe focal.

1.4 Equations réduites des quadriques propres

Définition : Il y a 5 types de quadriques propres :

Le paraboloïde elliptique $\left ( PE\right )$ d'équation réduite : $\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=\dfrac{2z}{c},\quad a>0,\; b>0,\; c\neq0$
Si , il est de révolution d'axe .
Le paraboloïde hyperbolique $\left( PH\right)$ d'équation réduite : $\dfrac{x^{2}}{a^{2}}-\dfrac{y^{2}}{b^{2}}=\dfrac{2z}{c},\quad a>0,\; b>0,\; c\neq0$
Il n'est jamais de révolution.
L'ellipsoïde $\left( E\right)$ d'équation réduite : $\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}+\dfrac{z^{2}}{c^{2}}=1,\quad a>0,\; b>0,\; c>0$
Si , il est de révolution d'axe .
L'hyperboloïde à une nappe $\left( H1\right)$ d'équation réduite : $\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}-\dfrac{z^{2}}{c^{2}}=1,\quad a>0,\; b>0,\; c>0$
Si , il est de révolution d'axe .
L'hyperboloïde à deux nappes $\left( H2\right)$ d'équation réduite : $\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}-\dfrac{z^{2}}{c^{2}}=-1,\quad a>0,\; b>0,\; c>0$
Si , il est de révolution d'axe .

On verra plus loin qu'on peut toujours faire un changement de repère orthonormal tel que dans ce repère l'équation d'une quadrique donnée est réduite.
Toutes, sauf le paraboloïde hyperbolique possédent une « version » de révolution.
On a ainsi facilement une description géométrique de ces quadriques en dilatant selon un ou deux axes la quadrique de révolution correspondante.

1.5 Le paraboloïde elliptique $\left ( PE\right )$

Equation réduite : 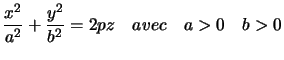$\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=2pz\quad avec\quad a>0\quad b>0$

Si $\quad a=b\quad$ il est de révolution d'axe , alors obtenu en faisant tourner une parabole autour de son axe de symétrie.
Il est formé de paraboles (intersection avec un plan vertical) et d'ellipses. L'intersection avec le plan tangent est réduite à un point.
Tout point est en ballon. Il ne contient pas de droites. Il n'y a pas non plus de centre de symétrie.
On obtient un paramétrage classique en s'inspirant des coordonnées cylindriques :

$\begin{displaymath} t\in\mathbb{R}^{+},\theta\in\left[ 0,2\pi\right] \left\{ \... ...t{ }t\sin\theta\\ z=\dfrac{t^{2}}{2p} \end{array} \right. \end{displaymath}$

Le paraboloïde elliptique est représenté ci-dessous.

$\includegraphics[width=10cm]{PE}$

1.6 Le paraboloïde hyperbolique $\mathbf{(}PH\mathbf{)}$

Equation réduite : $\dfrac{x^{2}}{a^{2}}-\dfrac{y^{2}}{b^{2}}=2pz\quad avec\quad a>0\quad b>0$

Il n'est jamais de révolution, mais contient deux familles de droites obtenues en factorisant

$\displaystyle \dfrac{x^{2}}{a^{2}}-\dfrac{y^{2}}{b^{2}}=\left( \dfrac{x}{a}-\dfrac{y} {b}\right) \left( \dfrac{x}{a}+\dfrac{y}{b}\right)$

ce qui donne : $\begin{displaymath}\left\{ \begin{array}[c]{l} \dfrac{x}{a}-\dfrac{y}{b}=k\\... ...c{x}{a}+\dfrac{y}{b}=\dfrac{2pz}{k} \end{array} \right. \quad\end{displaymath}$ et $\begin{displaymath}\left\{ \begin{array}[c]{l} \dfrac{x}{a}+\dfrac{y}{b}=k\\... ...c{x}{a}-\dfrac{y}{b}=\dfrac{2pz}{k} \end{array} \right. \quad\end{displaymath}$ avec non nul. L'intersection avec le plan tangent est formée de 2 droites.
Par tout point, il passe deux droites distinctes tracées sur la surface, intersection avec le plan tangent à ce point.
Tout point est en col. Il n'a pas de centre de symétrie. Il est formé d'hyperboles et de paraboles.
On obtient un paramétrage classique en s'inspirant des coordonnées cylindriques associées à de la trigonométrie hyperbolique : $\begin{displaymath} t\in\mathbb{R},\theta\in\mathbb{R}\left\{ \begin{array}[c]... ...\dfrac{x}{a}\right\vert >\left\vert \dfrac{y} {b}\right\vert \end{displaymath}$
On inverse ch et sh et le signe de pour $\left\vert \dfrac{x}{a}\right\vert <\left\vert \dfrac{y}{b}\right\vert$
Le paraboloïde hyperbolique est représenté ci-dessous.

$\includegraphics[]{PH}$

1.7 L'Ellipsoïde

Equation réduite centrée : $\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}+\dfrac{z^{2}}{c^{2}}=1\quad avec\quad a>0\quad b>0\quad c>0$

Si $\quad a=b\quad$ il est de révolution d'axe . Il est alors obtenu en faisant tourner une ellipse autour d'un de ses axes de symétrie.
L'intersection avec le plan tangent est réduite à un point. Il ne contient pas de droites.
Tout point est en ballon. L'origine est centre de symétrie. Il est formé d'ellipses.
On obtient un paramétrage classique en s'inspirant des coordonnées sphériques :

$\begin{displaymath} \theta\in\left[ 0,2\pi\right] ,\varphi\in\left[ -\dfrac{\pi... ...cos\varphi\sin\theta\\ z=c\sin\varphi \end{array} \right. \end{displaymath}$

L'ellipsoïde est représenté ci-dessous.

$\includegraphics[]{E}$

1.8 L'hyperboloïde à une nappe

Equation réduite centrée : 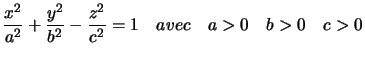$\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}-\dfrac{z^{2}}{c^{2}}=1\quad avec\quad a>0\quad b>0\quad c>0$

Si $\quad a=b\quad$ il est de révolution d'axe , alors obtenu en faisant tourner une hyperbole autour de son axe de symétrie non focal.
Le cône asymptote est d'équation : $\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}-\dfrac{z^{2}}{c^{2}}=0$
Il contient deux familles de droites obtenues en factorisant $\dfrac{x^{2} }{a^{2}}-\dfrac{z^{2}}{c^{2}}$ et $1-\dfrac{y^{2}}{b^{2}}$ comme différences de 2 carrés :

$\displaystyle \left( \dfrac{x}{a}-\dfrac{z}{c}\right) \left( \dfrac{x}{a}+\dfrac{z} {c}\right) =\left( 1-\dfrac{y}{b}\right) \left( 1+\dfrac{y}{b}\right)$

Ce qui donne : $\begin{displaymath}\left\{ \begin{array}[c]{l} \dfrac{x}{a}-\dfrac{z}{c}=k\lef... ...c{1}{k}\left( 1+\dfrac{y}{b}\right) \end{array} \right. \quad\end{displaymath}$ et $\begin{displaymath}\left\{ \begin{array}[c]{l} \dfrac{x}{a}+\dfrac{z}{c}=k\lef... ...c{1}{k}\left( 1+\dfrac{y}{b}\right) \end{array} \right. \quad\end{displaymath}$ avec non nul.
L'intersection avec le plan tangent est formée de 2 droites. Par tout point, il passe deux droites distinctes tracées sur la surface, intersection avec le plan tangent à ce point.
Tout point est un point col. L'origine est centre de symétrie. Il est formé d'ellipses, de paraboles et d'hyperboles.
On obtient un paramétrage classique en s'inspirant des coordonnées sphériques, et en utilisant de la trigonométrie hyperbolique : $\begin{displaymath} \varphi\in\mathbb{R},\theta\in\left[ 0,2\pi\right] \left\{... ...phi\sin\theta\\ z=c\text{ sh }\varphi \end{array} \right. \end{displaymath}$ L'hyperboloïde à une nappe est représenté ci-dessous.

$\includegraphics[]{H1}$

1.9 L'hyperboloïde à 2 nappes

Equation réduite centrée : $\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}-\dfrac{z^{2}}{c^{2}}=-1\quad avec\quad a>0\quad b>0\quad c>0$

Si $\quad a=b\quad$ il est de révolution d'axe , alors obtenu en faisant tourner une hyperbole autour de son axe focal.
Le cône asymptote est d'équation : $\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}-\dfrac{z^{2}}{c^{2}}=0$
L'intersection avec le plan tangent est réduite à un point. H2 ne contient pas de droites.
Tout point est en ballon. L'origine est centre de symétrie. Il est formé d'ellipses, de paraboles et d'hyperboles.
On obtient un paramétrage classique d'une seule des deux nappes en s'inspirant des coordonnées sphériques, et en utilisant de la trigonométrie hyperbolique : $\begin{displaymath} \varphi\in\mathbb{R},\theta\in\left[ 0,2\pi\right] \left\{... ...phi\sin\theta\\ z=c\text{ ch }\varphi \end{array} \right. \end{displaymath}$
L'hyperboloïde à deux nappes est représenté ci-dessous.

$\includegraphics[]{H2}$