Chapitre 2 : Compléments d'Algèbre linéaire
3 Eléments propres d'un endomorphisme
Sous-sections
Notation :  est un espace vectoriel sur
est un espace vectoriel sur 
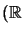 ou
ou  , de dimension finie ou non.
, de dimension finie ou non.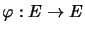 est un endomorphisme.
est un endomorphisme.
Définition :  et
et  est un couple valeur propre, vecteur propre de
est un couple valeur propre, vecteur propre de ![\begin{displaymath}\varphi\Leftrightarrow\left\{ \begin{array}[c]{l} u\neq0\\ \varphi\left( u\right) =\lambda.u \end{array} \right. \end{displaymath}](img57.png)
Remarque : Un vecteur propre n'est jamais nul.
Théorème :  est une valeur propre de
est une valeur propre de 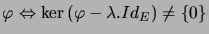
Définition : L'ensemble des valeurs propres de  est le spectre de
est le spectre de .
.
Définition : Si  est une valeur propre de
est une valeur propre de  , on appelle sous-espace propre de
, on appelle sous-espace propre de  associé à la valeur propre
associé à la valeur propre  ,
,

C'est donc l'ensemble des vecteurs propres associés à  auxquels on adjoint le vecteur nul.
auxquels on adjoint le vecteur nul.
Théorème : Le sous espace propre de  associé à la valeur propre
associé à la valeur propre ,
, 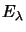 est un sous-espace vectoriel de
est un sous-espace vectoriel de  .
.
Preuve. est dons un sous espace vectoriel puisque c'est un noyau.
est dons un sous espace vectoriel puisque c'est un noyau. 
Remarque : On note  même quand
même quand  n'est pas valeur propre de
n'est pas valeur propre de  .
.
D'une façon plus particulière,  .
.
Ainsi, 0 est valeur propre  n'est pas injective.
n'est pas injective.
Théorème : 2 sous-espaces propres associés à des valeurs propres distinctes sont en somme directe.
Preuve. Soit  , alors
, alors  , d'où
, d'où  et comme
et comme ,
,  .
. 
Théorème :  un
un  -e.v.,
-e.v.,  ,
, valeurs propresdistinctes 2 à 2,
valeurs propresdistinctes 2 à 2, vecteurs propres associés, alors la famille
vecteurs propres associés, alors la famille  est libre.
est libre.
Preuve. On pose

à laquelle on applique 
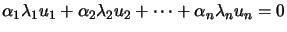
à laquelle on retire  fois la relation précédente, d'où :
fois la relation précédente, d'où :

Pour conclure, il suffit de remarquer que si  est libre, alors
est libre, alors  est libre.
est libre.
Comme  est libre, on a le résultat.
est libre, on a le résultat. 
- Homothétie de rapport
 Une homothétie de rapport
Une homothétie de rapport  possède une unique valeur propre
possède une unique valeur propre et
et 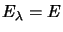 . Tous les vecteurs, sauf le vecteur nul, sont propres.
. Tous les vecteurs, sauf le vecteur nul, sont propres.
- Soit
 la projection sur
la projection sur  parallèlement à
parallèlement à  . 1 et 0 sont les deux valeurs propres,
. 1 et 0 sont les deux valeurs propres,  et
et  .
.
On écrit la décomposition canonique selon la somme directe d'un vecteur non nul, propre pour  ,
,  , à laquelle on applique
, à laquelle on applique , d'où
, d'où  ce qui donne
ce qui donne .
.
 et
et  ne sont pas tous les 2 nuls puisque
ne sont pas tous les 2 nuls puisque  ne l'est pas.
ne l'est pas.
Comme  ne peut à la fois être égal à 1 et à 0,
ne peut à la fois être égal à 1 et à 0,  et
et  sont liés et donc l'un des 2 est nul.
sont liés et donc l'un des 2 est nul.
Ce qui entraîne 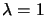 et
et ou
ou  et
et  . Il ne reste qu'à conclure.
. Il ne reste qu'à conclure. - Soit
 la symétrie par rapport à
la symétrie par rapport à  , parallèlement à
, parallèlement à . 1 et -1 sont les deux valeurs propres,
. 1 et -1 sont les deux valeurs propres,  et
et  .
.
Le résultat est immédiat en écrivant 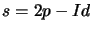 .
.
- Soit
![$ E=\mathcal{C}^{0}\left[ \mathbb{R}\right] $](img98.png) et
et 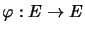 telle que
telle que 
En un mot,  est la primitive de
est la primitive de  qui s'annule en 0. On va chercher les éléments propres de
qui s'annule en 0. On va chercher les éléments propres de 
Il faut d'abord vérifier que  est bien un endomorphisme, c'est à dire que c'est une application de
est bien un endomorphisme, c'est à dire que c'est une application de  dans
dans  qui est linéaire.
qui est linéaire.
 est clairement continue puisque c'est une primitive d'une application continue.
est clairement continue puisque c'est une primitive d'une application continue.
De plus  est bien linéaire par linéarité de l'intégration,
est bien linéaire par linéarité de l'intégration,  est donc bien un endomorphisme.
est donc bien un endomorphisme.
Cherchons en les éléments propres, c'est à dire les applications non identiquement nulles et les scalaires
non identiquement nulles et les scalaires  tels que
tels que
On écrit cette égalité pour un 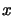 quelconque :
quelconque : ou encore
ou encore 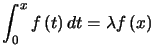 pour tout
pour tout 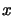 réel. Si
réel. Si  pour tout
pour tout 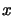 réel,
réel,  en dérivant,
en dérivant, 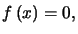
 est l'application nulle et n'est donc pas un vecteur propre, 0 n'est donc pas valeur propre.
est l'application nulle et n'est donc pas un vecteur propre, 0 n'est donc pas valeur propre.
Donc  d'où
d'où  est de classe
est de classe  sur
sur et en dérivant, pour tout
et en dérivant, pour tout 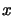 réel,
réel, 
On conserve la condition  pour avoir une équivalence.
pour avoir une équivalence. est donc solution de l'équation différentielle linéaire du premier ordre à coefficients constants sans second membre
est donc solution de l'équation différentielle linéaire du premier ordre à coefficients constants sans second membre  , ce qui donne
, ce qui donne 

La valeur en 0 nous donne  et donc
et donc  est encore l'application nulle...
est encore l'application nulle...
Finalement  n'a pas de valeur propre.
n'a pas de valeur propre.
© Christophe Caignaert - Lycée Colbert - Tourcoing![]() est un espace vectoriel sur
est un espace vectoriel sur ![]()
![]() ou
ou ![]() , de dimension finie ou non.
, de dimension finie ou non.![]() est un endomorphisme.
est un endomorphisme.![]() et
et ![]() est un couple valeur propre, vecteur propre de
est un couple valeur propre, vecteur propre de ![\begin{displaymath}\varphi\Leftrightarrow\left\{ \begin{array}[c]{l} u\neq0\\ \varphi\left( u\right) =\lambda.u \end{array} \right. \end{displaymath}](img57.png)
![]() est une valeur propre de
est une valeur propre de ![]()
![]() est le spectre de
est le spectre de![]() .
.![]() est une valeur propre de
est une valeur propre de ![]() , on appelle sous-espace propre de
, on appelle sous-espace propre de ![]() associé à la valeur propre
associé à la valeur propre ![]() ,
,![]()
![]() auxquels on adjoint le vecteur nul.
auxquels on adjoint le vecteur nul.![]() associé à la valeur propre
associé à la valeur propre![]() ,
, ![]() est un sous-espace vectoriel de
est un sous-espace vectoriel de ![]() .
.![]() est dons un sous espace vectoriel puisque c'est un noyau.
est dons un sous espace vectoriel puisque c'est un noyau. ![]()
![]() même quand
même quand ![]() n'est pas valeur propre de
n'est pas valeur propre de ![]() .
. ![]() .
. ![]() n'est pas injective.
n'est pas injective.![]() , alors
, alors ![]() , d'où
, d'où ![]() et comme
et comme![]() ,
, ![]() .
. ![]()
![]() un
un ![]() -e.v.,
-e.v., ![]() ,
,![]() valeurs propresdistinctes 2 à 2,
valeurs propresdistinctes 2 à 2,![]() vecteurs propres associés, alors la famille
vecteurs propres associés, alors la famille ![]() est libre.
est libre.![]()
![]()
![]()
![]() fois la relation précédente, d'où :
fois la relation précédente, d'où :![]()
![]() est libre, alors
est libre, alors ![]() est libre.
est libre. ![]() est libre, on a le résultat.
est libre, on a le résultat. ![]()
![]()

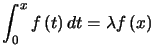 pour tout
pour tout  en dérivant,
en dérivant,