Chapitre 2 : Compléments d'Algèbre linéaire

4 Trace d'un endomorphisme et d'une matrice

Sous-sections

4 Trace d'un endomorphisme et d'une matrice

Notons d'abord que la notion de trace est hors programme mais très pratique...

4.1 Trace d'une matrice

Définition : La trace d'une matrice, notée tr $\left( A\right)$ , est la somme des éléments diagonaux. avec les notations classiques, pour une matrice $n\times n$ , on a :

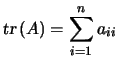
$\displaystyle \textsl{tr}\left( A\right) =\sum_{i=1}^{n}a_{ii}$

Exemple : La trace de $\begin{displaymath}\left( \begin{array}{ccc} 1 & 2 & 3 \\ 3 & 4 & 5 \\ 5 & 6 & 7 \end{array} \right) \end{displaymath}$ est .

Théorème : deux matrices $n\times n$ , alors,

$\displaystyle \textsl{tr}\left( AB\right) =\textsl{tr}\left( BA\right)$

Preuve. L'élément $i^{\grave{e}me}$ ligne et colonne de est $\sum\limits_{j=1}^{n}a_{ij} b_{ji}$ ,

$\displaystyle \textsl{tr}\left( AB\right) =\sum\limits_{i=1}^{n}\sum\limits_{j=... ...its_{i=1}^{n}\sum\limits_{j=1}^{n}b_{ij} a_{ji}=\textsl{tr}\left( BA\right)$

car les indices de sommation sont muets. $\qedsymbol$

Théorème : 2 matrices semblables ont la même trace.

Preuve. $A^{\prime}=P^{-1}AP$ ,

$\displaystyle \textsl{tr}\left( A^{\prime}\right) =\textsl{tr}\left( P^{-1}AP\r... ...P^{-1}\right) =\textsl{tr}\left( APP^{-1}\right) =\textsl{tr}\left( A\right)$

$\qedsymbol$

Exemple : Les deux matrices 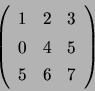$\begin{displaymath}\left( \begin{array}{ccc} 1 & 2 & 3 \\ 0 & 4 & 5 \\ 5 & 6 & 7 \end{array} \right) \end{displaymath}$ et $\begin{displaymath}\left( \begin{array}{ccc} 2 & 1 & 3 \\ 4 & 0 & 5 \\ 6 & 5 & 7 \end{array} \right)\end{displaymath}$ ne diffèrent que par l'interversion des deux premières colonnes mais ne sont pas semblables puisqu'elles n'ont pas la même trace !...

4.2 Trace d'un endomorphisme

Comme 2 matrices semblables ont la même trace, la trace d'un endomorphisme est définie comme la trace de sa matrice dans n'importe quelle base.