Définition : Soit ![]() , continue sur
, continue sur ![]() un ouvert de
un ouvert de ![]() . Une équation différentielle du premier ordre est une équation du type :
. Une équation différentielle du premier ordre est une équation du type :
| (1) |
Une solution de (1) est une fonction de classe ![]() sur
sur![]() un intervalle de
un intervalle de ![]() telle que :
telle que :
![]()
![]()
Théorème : On utilise les notations de la définition précédente. Si ![]() , il existe, sous certaines conditions, un intervalle
, il existe, sous certaines conditions, un intervalle ![]() et une solution unique sur
et une solution unique sur ![]() , vérifiant
, vérifiant![]() .
.
Une telle solution permet de définir unecourbe intégrale de (1).
Définition : L'équation (1) est dite à variables séparables lorsque, en posant 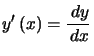 , (1) peut se mettre sous la forme :
, (1) peut se mettre sous la forme :
| (2) |
Théorème : On obtient une courbe intégrale de (2) en primitivant chacun de ses membres. Soit, en tenant compte des conditions initiales :
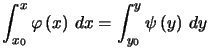
Ce qui entraine, en appelant ![]() et
et ![]() deux primitives respectives de
deux primitives respectives de![]() et
et ![]() :
:
![]()
En particulier, si l'équation (1) est incomplète, c'est à dire s'il manque ![]() ou
ou ![]() , alors, elle est à variables séparables :
, alors, elle est à variables séparables :
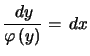 sur un intervalle où
sur un intervalle où Définition : ![\begin{displaymath}\left. \begin{array}[c]{l} \dfrac{\,dx}{\,dt}=\varphi(x,y)\\ \dfrac{\,dy}{\,dt}=\psi(x,y) \end{array} \right\} \end{displaymath}](img201.png) avec
avec ![]() et
et ![]() continues sur
continues sur ![]() un ouvert de
un ouvert de ![]() , est un système autonome de deux équations différentielles.
, est un système autonome de deux équations différentielles.
Une solution est appelée trajectoire du système autonome.
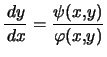 Cela revient à faire disparaître «
Cela revient à faire disparaître « 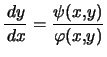 peut se transformer en système autonome en « ajoutant » du temps «
peut se transformer en système autonome en « ajoutant » du temps « Soit l'équation différentielle 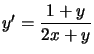 , on pose
, on pose![\begin{displaymath}\left\{ \begin{array}[c]{l} \dfrac{\,dx}{\,dt}=2x+y\\ \dfrac{\,dy}{\,dt}=1+y \end{array} \right. \end{displaymath}](img204.png) Il est facile d'intégrer cette dernière équation, cela donne :
Il est facile d'intégrer cette dernière équation, cela donne :![]() , valeur que l'on reporte dans la première :
, valeur que l'on reporte dans la première :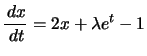 .
.
Il est encore facile d'intégrer cette équation, cela donne cette fois : 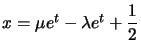 .
.
Finalement, on a les courbes intégrales en paramétriques : ![\begin{displaymath}\left\{ \begin{array}[c]{l} x=\mu e^{t}-\lambda e^{t}+\dfrac{1}{2}\\ y=\lambda e^{t}-1 \end{array} \right. \end{displaymath}](img208.png)