Chapitre 3 : Suites Récurrentes Linéaires

Le but est de déterminer toutes les suites $\left( u_{n}\right) _{n\in\mathbb{N}}$ qui vérifient

$\displaystyle \forall n\in\mathbb{N},\quad a\,u_{n+2}+b\,u_{n+1}+c\,u_{n}=d,\quad a,b,c,d\in \mathbb{K}$

(1)

On considère

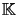l'espace vectoriel des suites sur $\mathbb{K}$ , et

$\begin{displaymath} \varphi:\left\{ \begin{array}[c]{rll} E & \rightarrow & E... ...{n+1}+c\,u_{n}\right) _{n\in\mathbb{N}} \end{array} \right. \end{displaymath}$

$\varphi$ est clairement linéaire. Il s'agit de résoudre

$\displaystyle \varphi\left( \left( u_{n}\right) _{n\in\mathbb{N}}\right) =\left( d\right) _{n\in\mathbb{N}}$

où $\left( d\right) _{n\in\mathbb{N}}$ est la suite constante. On se retrouve donc face à une équation linéaire. On va donc chercher les solutions de l'équation homogène associée :

$\displaystyle \forall n\in\mathbb{N},\quad a\,u_{n+2}+b\,u_{n+1}+c\,u_{n}=0$

Ces solutions forment un sous espace vectoriel de

. Il suffira d'ajouter une suite qui est solution particulière de $% latex2html id marker 901 $ \left( \ref{R}\right) $$ .