Chapitre 3 : Suites Récurrentes Linéaires

1 Suites vérifiant $u_{n+1}-a\,u_{n}=b$

Ce sont les suites géométriques de raison , $\forall n\in \mathbb{N},\quad u_{n}=a^{n}\,u_{0.}$

On cherche d'abord une solution particulière sous forme de suite constante $v_{n}=k$ , ce qui donne $\left( 1-a\right) k=b$ .

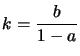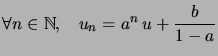Si $a\neq1$ , on trouve $k=\dfrac{b}{1-a}$ , et donc $\forall n\in\mathbb{N},\quad u_{n}=a^{n}\,u+\dfrac{b}{1-a}$ avec u qui se calcule en fonction des conditions initiales.
Si , la suite est arithmétique, $\forall n\in\mathbb{N},\quad u_{n}=u_{0}+nb$

Une fois qu'on a l'expression générale de la solution, on tient compte des conditions initiales éventuelles.