Chapitre 5 : Algèbre Bilinéaire, Produit Scalaire

1 Produit Scalaire sur

Sous-sections

1 Produit Scalaire sur

1.1 Forme bilinéaire symétrique sur

Définition : Soit $\begin{displaymath}\Psi:\left\{ \begin{array}[c]{ccc} E\times E & \rightarrow ... ...right) & \mapsto & \Psi\left( u,v\right) \end{array} \right. \end{displaymath}$
On dit que $\Psi$ est bilinéaire symétrique sur $\begin{displaymath}E\Leftrightarrow \left\{ \begin{array}[c]{l} \forall u\in ... ...\left( u,v\right) =\Psi\left( v,u\right) \end{array} \right. \end{displaymath}$

Théorème : Pour montrer qu'une forme est bilinéaire symétrique, il suffit de montrer qu'elle est linéaire par rapport à une variable, au choix, et qu'elle est symétrique.

Preuve. On sait $\begin{displaymath}\left\{ \begin{array}[c]{l} \forall\lambda,\mu\in\mathbb{R}... ...\left( u,v\right) =\Psi\left( v,u\right) \end{array} \right. \end{displaymath}$
D'où $\Psi\left( u,\lambda.v_{1}+\mu.v_{2}\right) =\Psi\left( \lambda.v_{1}+\mu.v_{... ...u\right) =\lambda \Psi\left( u,v_{1}\right) +\mu \Psi\left( u,v_{2}\right)$ en faisant jouer la symétrie et la linéarité par rapport à chaque variable.
On obtient bien la deuxième linéarité. $\qedsymbol$

1.2 Forme quadratique associée à une forme bilinéaire symétrique

Définition : Une forme quadratique sur $\mathbb{R}^n$ est une application de $\mathbb{R}^n\rightarrow\mathbb{R}$ qui se met sous la forme d'un polynôme homogène de degré 2 des coordonnées du vecteur de $\mathbb{R}^n$ .

Théorème : Si $\Psi$ est une forme bilinéaire symétrique sur , alors $\begin{displaymath}q:\left\{ \begin{array}[c]{l} E\rightarrow\mathbb{R}\\ u\... ... q\left( u\right) =\Psi\left( u,u\right) \end{array} \right. \end{displaymath}$ est une forme quadratique, c'est la forme quadratique associée à $\Psi$ .

Remarque : On a : $q\left( \lambda.u\right) =\lambda^{2} q\left( u\right)$ , ce qui prouve que n'est pas linéaire !

Théorème : Si une forme quadratique sur , alors $\Psi : E\times E \rightarrow \mathbb{R}$ définie par

$\displaystyle \Psi\left( u,v\right) =\dfrac{q\left( u+v\right) -q\left( u\right) -q\left( v\right) }{2}$

est une forme bilinéaire symétrique. On dit alors que $\Psi$ est la forme polaire de .

Preuve. La symétrie est évidente, on admet la bilinéarité.

$\displaystyle \dfrac{q\left( u+v\right) -q\left( u\right) -q\left( v\right) }{2}$	$\displaystyle =\dfrac{\Psi\left( u+v,u+v\right) -\Psi\left( u,u\right) -\Psi\left( v,v\right) }{2}$
	$\displaystyle =\dfrac{\left( \Psi\left( u,u\right) +\Psi\left( u,v\right) +\Ps... ...si\left( v,v\right) \right) -\Psi\left( u,u\right) -\Psi\left( v,v\right) }{2}$
	$\displaystyle =\dfrac{\Psi\left( u,v\right) +\Psi\left( v,u\right) }{2}$
	$\displaystyle =\Psi\left( u,v\right)$

$\qedsymbol$

1.3 Forme quadratique définie positive

Définition : une forme quadratique, on dit que est positive $\Leftrightarrow\forall u\in E, \; q\left( u\right) \geqslant0$ .

Définition : une forme quadratique positive, on dit que est définie-positive $\Leftrightarrow\forall u\in E,\left( q\left( u\right) =0\Leftrightarrow u=0\right)$ .
On dit aussi que est positive non-dégénérée.

Le même vocabulaire s'applique à la forme bilinéaire symétrique.

1.4 Produit Scalaire sur

Définition : Un produit scalaire sur est une forme bilinéaire symétrique définie positive sur
. $\Psi\left( u,v\right)$ se note le plus souvent $\left\langle u,v\right\rangle$ .

Exemple : Le produit scalaire usuel du plan ou de l'espace. La forme quadratique est alors le carré scalaire.

Remarque : Pour montrer que $\left\langle \cdot,\cdot\right\rangle$ est un produit scalaire, on montre successivement :

la linéarité par rapport à une variable,
la symétrie,
la positivité de la forme quadratique et enfin,
son caractère défini-positif.

Définition : Un espace vectoriel préhilbertien est un espace vectoriel muni d'un produit scalaire.

Remarque : Un espace vectoriel préhilbertien est donc un espace vectoriel réel. Il peut être de dimension finie ou infinie.

Définition : Un espace vectoriel euclidien est un espace vectoriel de dimension finie muni d'un produit scalaire.

Remarque : Un espace vectoriel euclidien est donc un espace vectoriel réel.

1.5 Exemples classiques

1.5.1 Produit scalaire défini par une intégrale

On va montrer que sur $\mathbb{R}\left[ X\right] ,$ $\left\langle P,Q\right\rangle =\displaystyle\int_{0}^{1}P\left( t\right) Q\left( t\right) dt$ est un produit scalaire.
Il faut d'abord montrer que c'est une forme bilinéaire symétrique, c'est à dire qu'elle est linéaire par rapport à la première variable et symétrique.
On considère des polynômes quelconques $P_{1},P_{2},Q$ et des scalaires quelconques $\lambda,\mu.$

$\left\langle \lambda P_{1}+\mu P_{2},Q\right\rangle =\lambda \left\langle P_{1},Q\right\rangle +\mu\left\langle P_{2},Q\right\rangle$ par simple linéarité de l'intégration.

$\left\langle P,Q\right\rangle =\left\langle Q,P\right\rangle$ car $P\left( t\right) Q\left( t\right) =Q\left( t\right) P\left( t\right)$ pour tout

Il faut ensuite montrer que la forme quadratique est positive puis définie-positive.
On considère un polynôme quelconque

$\left\langle P,P\right\rangle =\displaystyle\int_{0}^{1}P^{2}\left( t\right) dt\geqslant0$ par positivité de l'intégrale. La forme est positive.

$\left\langle P,P\right\rangle =\displaystyle\int_{0}^{1}P^{2}\left( t\right) dt=0$ implique que $\forall t\in\left[ 0.1\right] ,P^{2}\left( t\right) =0$ car c'est un polynôme, donc une application continue, qui est de plus positive et d'intégrale nulle (théorème des 3 conditions).
On a donc $\forall t\in\left[ 0.1\right] , P\left( t\right) =0$ et enfin, $\forall t\in\mathbb{R}, P\left( t\right) =0$ , c'est à dire car unpolynôme qui a une infinité de racines est nul.
La forme est donc bien définie positive.

Finalement, sur $\mathbb{R}\left[ X\right] ,$ $\left\langle P,Q\right\rangle =\displaystyle\int_{0}^{1}P\left( t\right) Q\left( t\right) dt$ est un produit scalaire.

1.5.2 Produit scalaire sur un espace de matrices

Montrons que $\left\langle A,B\right\rangle = tr\left( ^{t}\!AB\right)$ définit un produit scalaire sur $\mathcal{M}_n(\mathbb{R})$ .
Il faut montrer la linéarité par rapport à la première (ou la deuxième) variable, la symétrie, puis il faut montrer que la forme quadratique associée est positive, puis définie-positive.

$\left\langle A,\lambda B+\mu C\right\rangle =tr\left( ^{t}\!A(\lambda B+\mu C... ...\!AC\right) =\lambda tr\left( ^{t}\!AB\right) +\mu tr\left( ^{t}\!AC\right)$
Ce qui donne : $\left\langle A,\lambda B+\mu C\right\rangle =\lambda\left\langle A,B\right\rangle +\mu\left\langle A,C\right\rangle$ en utilisant la linéarité de la trace.

$\left\langle B,A\right\rangle =tr\left( ^{t}\!BA\right) =tr\left( ^{t}\!\left... ...}\!BA\right) \right) =tr\left( ^{t}\!AB\right) =\left\langle A,B\right\rangle$ , en utilisant le fait qu'une matrice et sa transposée ont la même trace.
La forme est donc bilinéaire symétrique.

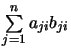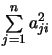$^{t}\!AB$ a pour coefficient $i^{\grave{e}me}$ ligne, $i^{\grave{e}me}$ colonne : $\sum\limits_{j=1}^{n}a_{ji}b_{ji}$ , celui de $^{t}\!AA$ est : $\sum\limits_{j=1}^{n}a_{ji}^{2}$ d'où : $\left\langle A,A\right\rangle ={\displaystyle\sum\limits_{i=1}^{n}}{\displayst... ...e\sum\limits_{i=1}^{n}}{\displaystyle\sum\limits_{j=1}^{n}}a_{ij}^{2}\geqslant0$ .
La forme est bien positive.
$\left\langle A,A\right\rangle =0\Rightarrow{\displaystyle\sum\limits_{i=1}^{n}... ...{j=1}^{n}}a_{ij}^{2}=0\Rightarrow\forall i,j\in\{1,2,\ldots,n\},\quad a_{i,j}=0$ et enfin .
La forme est définie positive.

On a bien un produit scalaire. De plus : $\left\Vert A\right\Vert ^{2}=\left\langle A,A\right\rangle ={\displaystyle\sum\limits_{i=1}^{n}} {\displaystyle\sum\limits_{j=1}^{n}}a_{ij}^{2}$ .

1.6 Inégalité de Cauchy-Schwarz (ou de Schwarz)

Théorème : $\left\langle \cdot,\cdot\right\rangle$ un produit scalaire sur , alors,

$\displaystyle \forall u,v\in E,\left\vert \left\langle u,v\right\rangle \right\... ...t \sqrt{\left\langle u,u\right\rangle }\sqrt{\left\langle v,v\right\rangle }$

L'égalité n'est vérifiée que si et sont liés.

Preuve. On a $\forall\lambda\in\mathbb{R}$ ,

$\displaystyle \left\langle u+\lambda.v,u+\lambda.v\right\rangle$	$\displaystyle \geqslant0$
$\displaystyle \left\langle v,v\right\rangle \lambda^{2}+2\left\langle u,v\right\rangle \lambda+\left\langle u,u\right\rangle$	$\displaystyle \geqslant0$

expression du second degré en $\lambda$ , qui ne change pas de signe, elle a donc un discriminant négatif, d'où : $\dfrac{\Delta}{4}=\left\langle u,v\right\rangle ^{2}-\left\langle v,v\right\rangle \left\langle u,u\right\rangle \leqslant0$
Ce qui assure le résultat.
Remarquons que l'égalité : $\left\vert \left\langle u,v\right\rangle \right\vert =\sqrt{\left\langle u,u\right\rangle }\sqrt{\left\langle v,v\right\rangle }$ ne se produit que si $\Delta=0$ , donc si $\left\langle v,v\right\rangle \lambda^{2}+2\left\langle u,v\right\rangle \lambda+\left\langle u,u\right\rangle =0$ pour un certain $\lambda$ .
Cela revient à $\left\langle u+\lambda .v,u+\lambda.v\right\rangle =0$ et enfin $u+\lambda.v=0$ , et sont liés. $\qedsymbol$

Exemple : On va appliquer l'inégalité de Schwarz avec le produit scalaire précédent et $Q\left( t\right) =t,$ compte tenu que $\displaystyle\int_{0} ^{1}t^{2}\,dt=\dfrac{1}{3},$ on obtient $\left( \displaystyle\int_{0}^{1}tP\left( t\right) dt\right) ^{2}\leqslant\dfrac{1}{3}\displaystyle\int_{0}^{1}P^{2}\left( t\right) dt$ qui est un résultat valable pour tout polynôme

On n'oubliera donc pas que l'inégalité de Schwarz permet de montrer de nombreuses inégalités « étonnantes ».