Définition : ![]() et
et ![]() sont orthogonaux pour
sont orthogonaux pour ![]()
Exemple : ![$ E=\mathcal{C}^{0}\left( \left[ 0,2\pi\right] \right) ,\left\langle f,g\right\rangle =\displaystyle\int_{0}^{2\pi}f\left( t\right) g\left( t\right) dt$](img93.png) , alors
, alors ![\begin{displaymath}\left\{ \begin{array}[c]{c} f:t\rightarrow\sin t\\ g:t\rightarrow\cos t \end{array} \right. \end{displaymath}](img94.png) sont orthogonales.
sont orthogonales.
En effet, c'est encore le théorème des 3 conditions qui permet de prouver qu'on a encore affaire à un produit scalaire et ![$ \displaystyle\int_{0}^{2\pi }\sin t\cos t\,dt=\left[ \dfrac{1}{2}\sin^{2}t\right] _{0}^{2\pi}=0,$](img95.png)
ce qui prouve l'orthogonalité.
Remarque : Le vecteur nul est orthogonal à tous les vecteurs.
Théorème : Soit ![]() une partie non vide de
une partie non vide de ![]() , préhilbertien,
, préhilbertien,
![]()
est un sous espace vectoriel de ![]() .
.
Si ![]() ne contient qu'un seul vecteur
ne contient qu'un seul vecteur ![]() , on le note alors
, on le note alors ![]() .
.
Preuve.![]() est clairement non vide. Montrons qu'il est stable par combinaison linéaire.
est clairement non vide. Montrons qu'il est stable par combinaison linéaire.
Soit ![\begin{displaymath}\left\{ \begin{array}[c]{l} u_{1},u_{2}\in A^{\perp}\\ \lambda,\mu\in\mathbb{R}\\ v\in A \end{array} \right. \end{displaymath}](img100.png) , alors
, alors ![]() .
.
Comme ![]() est quelconque, ceci prouve que
est quelconque, ceci prouve que ![]() qui est donc un sous espace vectoriel.
qui est donc un sous espace vectoriel. ![]()
Exemple : Dans ![]() muni du nouveau produit scalaire (admis)
muni du nouveau produit scalaire (admis)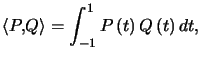 on va chercher l'orthogonal de l'ensemble
on va chercher l'orthogonal de l'ensemble ![]() des polynômes pairs, dont on admet qu'il constitue un sous-espace vectoriel.
des polynômes pairs, dont on admet qu'il constitue un sous-espace vectoriel.
Soit ![]() est un polynôme quelconque orthogonal à tous les polynômes pairs.
est un polynôme quelconque orthogonal à tous les polynômes pairs.
On considère ![]() et
et ![]() définis par
définis par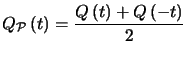 et
et 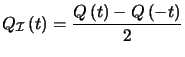 qui sont respectivement pairs et impairs. On a
qui sont respectivement pairs et impairs. On a ![]()
Soit ![]() un polynôme pair quelconque.
un polynôme pair quelconque.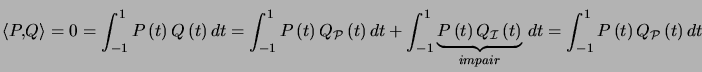
En prenant ![]() on obtient en utilisant encore le théorème des 3 conditions
on obtient en utilisant encore le théorème des 3 conditions ![]() et donc
et donc ![]() est impair.
est impair.
Comme tout polynôme impair convient, l'othogonal de l'ensemble![]() des polynômes pairs est l'ensemble des polynômes impairs.
des polynômes pairs est l'ensemble des polynômes impairs.
Théorème : ![]()
Preuve. Il est clair que ![]()
D'autre part, soit ![]()
![]()
On a donc ![]() ou encore
ou encore ![]()
![]()
Définition : Une famille ![]() de vecteurs estorthogonale
de vecteurs estorthogonale ![]() deux vecteurs quelconques de cette famille,
deux vecteurs quelconques de cette famille, ![]() , pour
, pour ![]() sont orthogonaux.
sont orthogonaux.
Définition : Une famille ![]() de vecteurs estorthonormale
de vecteurs estorthonormale ![]()
![\begin{displaymath}\left\{ \begin{array}[c]{l} \text{deux vecteurs quelconques... ... \left\Vert u_{i}\right\Vert =1\right) . \end{array} \right. \end{displaymath}](img125.png)
Remarque : On passe d'une famille orthogonale de vecteurs non nuls à une famille orthonormale en normant chaque vecteur.
Théorème : Tout famille orthonormale ou toute famille orthogonale de vecteurs non nuls est libre.
Preuve. Soit ![]() , on fait le produit scalaire par
, on fait le produit scalaire par ![]() , tous les
, tous les ![]() sont nuls sauf
sont nuls sauf ![]() d'où
d'où ![]() . Par récurrence immédiate, tous les
. Par récurrence immédiate, tous les![]() sont nuls, la famille est libre.
sont nuls, la famille est libre. ![]()
Théorème : Soit ![]() une famille libre de vecteurs de
une famille libre de vecteurs de ![]() préhilbertien, alors, il existe une famille
préhilbertien, alors, il existe une famille ![]() orthonormale de vecteur telle que
orthonormale de vecteur telle que
![]()
Preuve. Il suffit de fabriquer une famille orthonormale ![]() , la dimension de
, la dimension de![]() étant
étant ![]() , les
, les![]() sont non nuls.
sont non nuls.
La démonstration repose sur le fait qu'on ne change pas l'espace vectoriel engendré par une famille
La démonstration se fait par récuurence sur ![]() . Pour
. Pour ![]() ,
, ![]() convient.
convient.
On l'admet au rang ![]() , on le montre au rang
, on le montre au rang ![]() .
.
|
|
|
|
|
|
Soit ![]() avec
avec 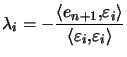 , alors
, alors ![]() pour
pour ![]() .
.
On pose 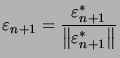 avec toujours les mêmes orthogonalités.
avec toujours les mêmes orthogonalités.
Et donc
|
|
|
|
|
|
La famille ![]() est bien orthonormale.
est bien orthonormale. ![]()
Corollaire : Tout espace vectoriel euclidien, ou tout sous espace vectoriel de dimension finie d'un espace préhilbertien possède au moins une base orthonormale.
Preuve. On applique le théorème de Schmidt à une base quelconque. ![]()
En pratique, la démonstration du théorème nous guide vers le procédé de Schmidt :
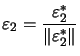 C'est le deuxième vecteur de la base orthonormale.
C'est le deuxième vecteur de la base orthonormale. ![\begin{displaymath}\left\{ \begin{array}[c]{l} \left\langle \varepsilon_{3}^{\... ...}^{\ast},\varepsilon_{2}\right\rangle =0 \end{array} \right. \end{displaymath}](img160.png) , d'où
, d'où ![\begin{displaymath}\left\{ \begin{array}[c]{l} \lambda=-\left\langle e_{3},\va... ...angle e_{3},\varepsilon_{2}\right\rangle \end{array} \right. \end{displaymath}](img161.png)
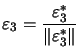 C'est le troisième vecteur de la base orthonormale.
C'est le troisième vecteur de la base orthonormale. Exemple : Dans ![]() muni du nouveau produit scalaire (admis)
muni du nouveau produit scalaire (admis) 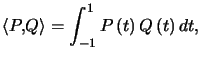 on va chercher une base orthonormale.
on va chercher une base orthonormale.
On part de la base ![]()
On a ![]() puis
puis 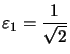 le premier vecteur normé, ceci par un calcul simple.
le premier vecteur normé, ceci par un calcul simple.![]() on écrit
on écrit ![]() et on obtient
et on obtient 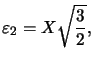 encore par un calcul simple.
encore par un calcul simple.![]() on écrit
on écrit ![]() d'où
d'où 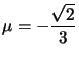 et
et ![]()
D'où 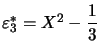 qu'il suffit de normer pour obtenir
qu'il suffit de normer pour obtenir 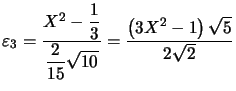
On voit que le calcul devient vite complexe...
Théorème : ![]() un espace vectoriel préhilbertien,
un espace vectoriel préhilbertien, ![]() un sous espace vectoriel de dimension finie muni d'une base orthonormale
un sous espace vectoriel de dimension finie muni d'une base orthonormale ![]() .
.
Alors
![]()
définit un projecteur.
Et comme ![]() , on dit que
, on dit que ![]() est la projection orthogonale sur
est la projection orthogonale sur ![]() .
.
La figure ci-dessous illustre ce théorème.
Preuve. Pour montrer que ![]() , il suffit de montrer qu'il est orthogonal à chaque
, il suffit de montrer qu'il est orthogonal à chaque ![]() .
.
|
|
|
|
|
|
car tous les autres termes sont nuls. D'où
![]()
![]() est clairement linéaire par linéarité du produit scalaire par rapport à la première variable.
est clairement linéaire par linéarité du produit scalaire par rapport à la première variable.
Il reste à montrer que ![]() est un projecteur, c'est à dire
est un projecteur, c'est à dire ![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
car ![]() . D'où
. D'où
![]()
et enfin
![]()
Lorsque ![]() est de dimension finie, on montre facilement que
est de dimension finie, on montre facilement que ![]() et
et ![]() est la projection sur
est la projection sur ![]() parallèlement à
parallèlement à ![]() , on appelle souvent
, on appelle souvent ![]() la projection sur
la projection sur ![]() parallèlement à
parallèlement à ![]() , on a alors
, on a alors ![]() .
. ![]()
En pratique, comme il faut une base orthonormale du sous espace sur lequel on projette, on cherchera ![]() si
si ![]() , et
, et ![]() sinon.
sinon.
On projette sur le plus petit...
Exemple : Dans ![]() muni du produit scalaire usuel, on cherche
muni du produit scalaire usuel, on cherche ![]() la projection orthogonale sur le plan
la projection orthogonale sur le plan ![]() d'équation
d'équation ![]()
![\begin{displaymath}P^{\bot}=Vect\left( \left( \begin{array}[c]{c} 1\\ 1\\ -1 \end{array} \right) \right) \end{displaymath}](img201.png) de base orthonormale
de base orthonormale ![\begin{displaymath}\left( \begin{array}[c]{c} 1/\sqrt{3}\\ 1/\sqrt{3}\\ -1/\sqrt{3} \end{array} \right) \end{displaymath}](img202.png)
Avec ![\begin{displaymath}u=\left( \begin{array}[c]{c} x\\ y\\ z \end{array} \right) ,\end{displaymath}](img203.png) on a
on a ![\begin{displaymath}q\left( u\right) =\left\langle u,\left( \begin{array}[c]{c}... ...ft( \begin{array}[c]{c} 1\\ 1\\ -1 \end{array} \right) \end{displaymath}](img204.png)
D'où ![\begin{displaymath}p\left( u\right) =u-q\left( u\right) =\left( \begin{array}[c... ...ay}[c]{c} 2x-y+z\\ -x+2y+z\\ x+y+2z \end{array} \right) \end{displaymath}](img205.png)
La matrice de cette projection dans la base canonique est donc :![\begin{displaymath}\dfrac{1}{3} \left( \begin{array}[c]{rrr} 2 & -1 & 1\\ -1 & 2 & 1\\ 1 & 1 & 2 \end{array} \right) \end{displaymath}](img206.png)