Chapitre 5 : Algèbre Bilinéaire, Produit Scalaire

6 Endomorphismes Symétriques et Applications

Sous-sections

6 Endomorphismes Symétriques et Applications

6.1 Endomorphismes symétriques

Définition : un espace vectoriel euclidien, $\varphi\in\mathcal{L}\left( E\right)$ ,

$\displaystyle \varphi$ est symétrique $\displaystyle \Leftrightarrow\forall u,v\in E,\left\langle \varphi\left( u\right) ,v\right\rangle =\left\langle u,\varphi\left( v\right) \right\rangle$

Théorème : Un endomorphisme est symétrique $\Leftrightarrow$ sa matrice dans une base orthonormale est symétrique.

Remarque : On ne sait rien de la matrice d'un endomorphisme symétrique dans une base quelconque.

Preuve. $\varphi$ symétrique a pour matrice $A=\left( a_{i,j}\right) _{1\leqslant i,j\leqslant n}$ dans $\mathcal{B}=\left( e_{1},\ldots ,e_{n}\right)$ orthonormale.
Les coordonnées de et sont les vecteurs colonnes et .

$\displaystyle \left\langle \varphi\left( u\right) ,v\right\rangle = ^{t}\!\lef... ...!U ^{t}\!AV= ^{t}\!UAV=\left\langle u,\varphi\left( v\right) \right\rangle$

D'où $a_{i,j}=\left\langle e_{i},\varphi\left( e_{j}\right) \right\rangle$ et $a_{j,i}=\left\langle \varphi\left( e_{i}\right) ,e_{j}\right\rangle$ ce qui prouve que est symétrique.
Réciproquement, si est symétrique, $^{t}\!A=A$ et clairement $\left\langle \varphi\left( u\right) ,v\right\rangle =\left\langle u,\varphi\left( v\right) \right\rangle$ . $\qedsymbol$

Théorème : un espace vectoriel euclidien, $\varphi\in\mathcal{L}\left( E\right)$ , $\varphi$ symétrique, alors $\varphi$ est diagonalisable au besoin dans une base orthonormale de vecteurs propres.

Preuve. On ne montre que le plus facile, le reste est admis.
On montre que si et sont propres pour des valeurs propres distinctes, ils sont orthogonaux.

$\displaystyle \left\langle \varphi\left( u\right) ,v\right\rangle =\left\langle... ...\rangle =\left\langle u,\mu.v\right\rangle =\mu\left\langle u,v\right\rangle$

D'où : $\left( \lambda-\mu\right) \left\langle u,v\right\rangle =0$ . $\qedsymbol$

Corollaire : une matrice symétrique réelle, est diagonalisable avec au besoin une matrice de passage orthogonale.

Ceci peut éviter bien des calculs puisque $P^{-1}= ^{t}\!P$ .

Remarque : Il est donc souvent intéressant de chercher à diagonaliser une matrice symétrique réelle dans une base orthonormale de vecteurs propres quand on a besoin de $P^{-1}$ .

6.2 Réduction d'une forme quadratique dans une base orthonormale

Une forme quadratique, ou une forme bilinéaire symétrique a une matrice symétrique réelle.
Il existe donc une base orthonormale où la matrice de la forme est diagonale.
Si dans cette base a pour coordonnées $\begin{displaymath}U=\left( \begin{array}[c]{c} x_{1}\\ x_{2}\\ \vdots\\ x_{n} \end{array} \right) \end{displaymath}$ , $q\left( u\right) =\lambda_{1} x_{1}^{2}+\lambda_{2} x_{2} ^{2}+\cdots+\lambda_{n} x_{n}^{2}$ .

Théorème : Une matrice symétrique réelle est une matrice de produit scalaire $\Leftrightarrow$ toutes les valeurs propres sont strictement positives.

Preuve. Cela revient à ce que la forme quadratique soit définie positive. Et pour cela, on utilise la remarque précédente. $\qedsymbol$

6.3 Identification d'une conique

On va utiliser la réduction des formes quadratiques dans le cas où il y a des temes en dans l'équation.
On part d'un polynôme non nul effectivement du second degré en et. (la forme quadratique n'est pas nulle).

6.3.1 Cas où il n'y a pas de termes en

avaler, si possible, les termes en et en dans des carrés par la transformation habituelle : $\left( x^{2}+ax=\left( x+\dfrac{a}{2}\right) ^{2}-\dfrac{a^{2}}{4}\right)$ .
Cela revient à faire une translation de l'origine du repère.
se ramener ensuite à une des formes canoniques décrites.
- On trouve des paraboles, hyperboles et ellipses (ou cercles)
- mais aussi des coniques dégénérées : couple de droites, droite, point, vide.

6.3.2 Cas où il y a des termes en

on repère la forme quadratique formée des termes du second degré $a x^{2}+2 b x y+c y^{2}$ on considère sa matrice $\begin{displaymath}\left( \begin{array}[c]{cc} a & b\\ b & c \end{array} \right)\end{displaymath}$ qu'on diagonalise dans une base orthonormale directe de vecteurs propres, avec la matrice de passage et $\lambda$ et $\mu$ les deux valeurs propres.
Cela revient à faire une rotation du repère.
alors $a x^{2}+2 b x y+c y^{2}=\lambda X^{2}+\mu Y^{2}$ avec $\begin{displaymath}\left( \begin{array}[c]{c} x\\ y \end{array} \right) =P\left( \begin{array}[c]{c} X\\ Y \end{array} \right)\end{displaymath}$ qui nous sert aussi à transformer le reste de l'équation de la conique.
il n'y a donc plus de termes en dans ce repère. On est ramené au cas précédent.

Remarque : Dans tous les cas, avec les notations précédentes où $\lambda$ et $\mu$ sont les valeurs propres de la forme quadratique, on peut conclure sur le type de conique obtenu.

$\lambda \mu>0\quad$ On a une ellipse, éventuellement dé générée (un point, le vide).

$\lambda \mu<0\quad$ On a une hyperbole, éventuellement dégénérée (deux doites sécantes).

$\lambda \mu=0\quad$ On a une parabole, éventuellement dégénérée (deux doites parallèles, une droite).

Ensuite, on opère la réduction habituelle du programme de première anné ...

6.4 Petits rappels sur les coniques

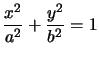
6.4.1 Ellipse : équation réduite centrée $\dfrac{x^{2}} {a^{2}}+\dfrac{y^{2}}{b^{2}}=1$

et avec sont les demi grand axe et demi petit axe.
Les foyers sont alors sur
$c=\sqrt{a^{2}-b^{2}}\quad$ est la distance du centre aux foyers
$e=\dfrac{c}{a}\quad$ est l'excentricité

La figure ci-dessous explicite les éléments géométriques de l'ellipse.

$\includegraphics[$

6.4.2 Parabole : équation réduite $y^{2}=2px\quad$ avec $p>0\quad$ le paramètre

est le sommet et l'axe de symétrie
l'excentricité vaut 1 et l'unique foyer est à la distance $\dfrac{p}{2}$ du sommet sur l'axe de symétrie

6.4.3 Hyperbole : équation réduite centrée $\dfrac{x^{2} }{a^{2}}-\dfrac{y^{2}}{b^{2}}=1$

les foyers sont alors sur
$c=\sqrt{a^{2}+b^{2}}\quad$ est la distance du centre aux foyers
$e=\dfrac{c}{a}\quad$ est l'excentricité
les asymptotes sont d'équation $\dfrac{x^{2}}{a^{2}} -\dfrac{y^{2}}{b^{2}}=\left( \dfrac{x}{a}-\dfrac{y}{b}\right) \left( \dfrac{x}{a}+\dfrac{y}{b}\right) =0$

La figure ci-dessous explicite les éléments géométriques de l'hyperbole.

$\includegraphics[$

6.4.4 Exemples de réduction

Exemple : On va d'abord retrouver la nature de la conique d'équation dans le repère orthonormal $\left( O,\overrightarrow{i},\overrightarrow {j}\right)$ .
On réécrit cette équation .
La forme quadratique a alors pour matrice $\begin{displaymath}\left( \begin{array}[c]{cc} 0 & 1\\ 1 & 0 \end{array} \right) \end{displaymath}$ dont les valeurs propres sont et
Les vecteurs propres associés sont : $\begin{displaymath}\left( \begin{array}[c]{c} 1\\ 1 \end{array} \right) \end{displaymath}$ et $\begin{displaymath}\left( \begin{array}[c]{c} -1\\ 1 \end{array} \right) \end{displaymath}$ . $\begin{displaymath}P=\dfrac{\sqrt{2}}{2}\left( \begin{array}[c]{cc} 1 & -1\\ 1 & 1 \end{array} \right) \end{displaymath}$ est orthogonale directe, et représente une rotation de centre et d'angle $\dfrac{\pi}{4}$ .
Dans le nouveau repère, tourné de $\dfrac{\pi}{4}$ , $2 x y=X^{2} -Y^{2}=2$ .
On a bien une hyperbole !

Exemple : On va identifier la conique d'équation $4 x^{2}+4 x y+y^{2}-2 x+4 y=0$ dans le repère orthonormal $\left( O, \overrightarrow{i}, \overrightarrow{j}\right)$ .
La forme quadratique a alors pour matrice : $\begin{displaymath}\left( \begin{array}[c]{cc} 4 & 2\\ 2 & 1 \end{array} \right) \end{displaymath}$ dont les valeurs propres sont 0 et 5.
Les vecteurs propres associés sont : $\begin{displaymath}\left( \begin{array}[c]{c} 1\\ -2 \end{array} \right) \end{displaymath}$ et $\begin{displaymath}\left( \begin{array}[c]{c} 2\\ 1 \end{array} \right) \end{displaymath}$ . $\begin{displaymath}P=\dfrac{\sqrt{5}}{5}\left( \begin{array}[c]{cc} 1 & 2\\ -2 & 1 \end{array} \right) \end{displaymath}$ est orthogonale directe, et représente une rotation de centre et d'angle $-\arccos\dfrac{\sqrt{5}}{5}$ .
Dans le nouveau repère, tourné de $-\arccos\dfrac{\sqrt{5}}{5}$ , $4 x^{2}+4 x y+y^{2}=5 Y^{2}$ .
D'autre part, $\begin{displaymath}\left( \begin{array}[c]{c} x\\ y \end{array} \right) =\... ...ht) \left( \begin{array}[c]{c} X\\ Y \end{array} \right) \end{displaymath}$ donne facilement : $-2 x+4 y=-2 X\sqrt{5}$ .
Finalement, l'équation dans le nouveau repère est $5 Y^{2}-2 X\sqrt {5}=0$ qui est une parabole d'axe , de sommet et de paramètre $\dfrac{\sqrt{5}}{5}$ .