Chapitre 6 : Fonctions de plusieurs variables, Continuité

1 Espace Vectoriel Normé $\mathbb{R}^{p}$

Sous-sections

1 Espace Vectoriel Normé $\mathbb{R}^{p}$

1.1 Norme et distance associée

En pratique, on n'utilisera que la norme euclidienne et sa distance associée.

Définition : $\begin{displaymath}\left\{ \begin{array}[c]{lll} E & \rightarrow & \mathbb{R}_... ... u & \mapsto & \left\Vert u\right\Vert \end{array} \right. \end{displaymath}$ est une norme $\begin{displaymath}\Leftrightarrow\left\{ \begin{array}[c]{l} \forall u,v\in E... ...ftrightarrow u=0\text{ (s\'{e}paration)} \end{array} \right. \end{displaymath}$
La norme d'un vecteur est souvent notée $\left\Vert u\right\Vert$

Remarque : Même si on parle souvent de la norme d'un vecteur, on verra qu'il y a une infinité de normes différentes...

Exemple :

$E=\mathbb{R}^{2}$ , $\begin{displaymath}\left\{ \begin{array}[c]{l} \left\Vert \left( x,y\right) \r... ...t\vert ,\left\vert y\right\vert \right) \end{array} \right. \end{displaymath}$

$\mathbb{R}^{p}$ a une structure euclidienne canonique, et si $u=\left( x_{1},x_{2},\ldots,x_{p}\right)$ ,

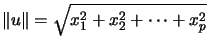
$\displaystyle \left\Vert u\right\Vert =\sqrt{x_{1}^{2}+x_{2}^{2}+\cdots+x_{p}^{2}}$

cette norme est appelée norme euclidienne. Sauf mention contraire, c'est elle qu'on utilise.

Définition : $d:\mathbb{R}^{p}\times\mathbb{R}^{p}\rightarrow\mathbb{R}_{+}$ est unedistance $\begin{displaymath}\Leftrightarrow\left\{ \begin{array}[c]{l} d\left( u,v\righ... ...ftrightarrow u=v\text{ (s\'{e}paration)} \end{array} \right. \end{displaymath}$

Théorème : $d\left( u,v\right) =\left\Vert v-u\right\Vert$ est une distance.

Preuve. prouve la symétrie. prouve l'inégalité triangulaire.
La séparation de la norme prouve enfin la séparation de la distance associée. $\qedsymbol$

Toute norme induit donc une distance, par contre, toute distance ne provient pas d'une norme.
On peut citer par exemple la distance ultramétrique : $d\left( u,v\right) =1$ pour $u\neq v$ et $d\left( u,u\right) =0$ .
Encore une fois, sauf mention contraire, on utilise la distance induite par la norme euclidienne.
Signalons que dans tout le reste du chapitre, on a souvent préféré la notion de norme, plus habituelle.
Cependant, on peut remplacer dans les expressions en $\varepsilon$ les normes par les distances correspondantes.

1.2 Boules, parties bornées, parties ouvertes ou fermées

Définition : Une boule ouverte de centre $u_{0}$ et de rayon est :

$\displaystyle B_{O}\left( u_{0},r\right) =\left\{ v\in\mathbb{R}^{p}, d\left( u_{0},v\right) <r\right\}$

Définition : Une boule fermée de centre $u_{0}$ et de rayon est :

$\displaystyle B_{F}\left( u_{0},r\right) =\left\{ v\in\mathbb{R}^{p}, d\left( u_{0},v\right) \leqslant r\right\}$

Définition : Une partie bornée de $\mathbb{R}^{p}$ est une partie de $\mathbb{R}^{p}$ incluse dans une certaine boule (ouverte ou fermée).

Définition : Une partie ouverte ou un ouvert de $\mathbb{R}^{p}$ est une partie telle que

$\displaystyle \forall u\in A,\quad\exists r>0,\quad B_{O}\left( u,r\right) \subset A$

C'est à dire que tout point de est le centre d'une boule ouverte, de rayon non nul, complètement incluse dans .

Définition : Une partie fermée ou un fermé de $\mathbb{R}^{p}$ est une partie telle que son complémentaire soit un ouvert.

Remarque : Une boule ouverte est un ouvet, une boule fermée est un fermé. $\mathbb{R}^{p}$ et $\emptyset$ sont ouverts et fermés.