Théorème : L'ensemble des applications ![]() , avec
, avec ![]() non vide,
non vide, ![]() , muni de
, muni de![\begin{displaymath} % latex2html id marker 3073 \left\{ \begin{array}[c]{l} \t... ...duit de 2 applications, not\'{e} }\times \end{array} \right. \end{displaymath}](img86.png) a une structure d'algèbre commutative sur
a une structure d'algèbre commutative sur ![]() .
.
Preuve. On en profite pour rappeler avec les notations du théorème la définition d'une algèbre, car toutes les démonstrations sont élémentaires..![]() est un espace vectoriel usuel.
est un espace vectoriel usuel.![]() est un anneau commutatif, car
est un anneau commutatif, car
![]()
![]()
Définition : ![]() , on dit que
, on dit que ![]() est bornée sur
est bornée sur ![]()
Soit ![]() , non vide. Soit
, non vide. Soit ![]() tel que
tel que
![]()
On ne s'intéressera à la limite de ![]() qu'en de tels points. Intuitivement, on peut dire que ces points de
qu'en de tels points. Intuitivement, on peut dire que ces points de ![]() ne sont pas des points « isolés ».
ne sont pas des points « isolés ».
Si, de plus, ![]() , on pourra s'intéresser à la continuité en un tel point.
, on pourra s'intéresser à la continuité en un tel point.
Définition : Dans les conditions précédentes, on dit que
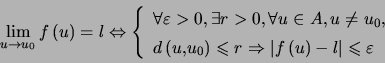
Définition : Dans ces mêmes conditions, on dit que ![]() est continue en
est continue en ![]() .
.
Définition : On dit que ![]() est continue sur
est continue sur ![]() est continue en tout vecteur
est continue en tout vecteur ![]() de
de ![]() .
.
L'ensemble des applications continues de ![]() , non vide, dans
, non vide, dans ![]() , se note
, se note ![]() .
.
Théorème : ![]() a une structure d'algèbre commutative, sous algèbre de
a une structure d'algèbre commutative, sous algèbre de ![]() .
.
Preuve. On en profite pour rappeler avec les notations du théorème, les conditions pour avoir une sous algèbre.
La fonction constante 1 est bien continue sur ![]() et appartient à
et appartient à![]() .
.
Ensuite, si ![]() et
et ![]() sont continues sur
sont continues sur ![]() , et
, et ![]() , alors
, alors ![]() ,
, ![]() , et
, et ![]() sont continues sur
sont continues sur ![]() , car la propriété est vraie en chaque vecteur
, car la propriété est vraie en chaque vecteur ![]() de
de ![]() .
.
La démonstration est la même que pour les fonctions de variable réelle en remplaçant certaines valeurs absolues par des normes. ![]()
Théorème : Si ![]() , alors
, alors ![]() est continue en tout vecteur
est continue en tout vecteur ![]() de
de ![]() tel que
tel que ![]() .
.
Théorème : Les applications « composantes » : ![]() sont continues sur
sont continues sur ![]() .
.
On utilise toujours les notations des paragraphes précédents. Le critère séquentiel est un critère reliant la limite d'une fonction en un point et des limites de suites.
Théorème : (critère séquentiel)
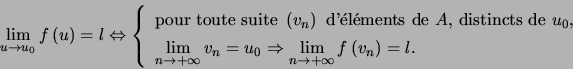
Preuve.
![]() Soit
Soit ![]() ,
,![]() mais
mais ![]() , d'où pour
, d'où pour ![]() ,
,![]() ce qui donne :
ce qui donne :![]()
en résumé,
![]()
Ceci prouve bien que ![]() .
.
![]() On va en fait montrer la contraposée. On sait
On va en fait montrer la contraposée. On sait
![]() et
et![]()
Soit ![]() , on forme une suite
, on forme une suite ![]() qui converge vers
qui converge vers ![]() et telle que
et telle que ![]() ne converge pas vers
ne converge pas vers ![]() .
.
Pour cela on prend simplement 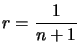 et on appelle
et on appelle ![]() le
le ![]() trouvé en appliquant ce qu'on sait.
trouvé en appliquant ce qu'on sait.
Clairement, on a : ![]() et
et ![]() quand
quand ![]() car on a toujours
car on a toujours ![]() .
.
![]()
Remarque : Ce théorème sert souvent à montrer que ![]() n'a pas de limite en
n'a pas de limite en![]() , en cherchant astucieusement de « bonnes » suites
, en cherchant astucieusement de « bonnes » suites ![]() .
.
Corollaire : ![]() continue en
continue en ![\begin{displaymath}u_{0}\Leftrightarrow\left\{ \begin{array}[c]{l} \text{pour ... ...t( v_{n}\right) =f\left( u_{0}\right) . \end{array} \right. \end{displaymath}](img132.png)
Exemple : On cherche la limite en ![]() de
de ![]()
Cette fonction est définie et continue sur ![]() par application des théorèmes élémentaires.
par application des théorèmes élémentaires.![]() et
et 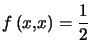 prouve que
prouve que![]() n'a pas de limite en
n'a pas de limite en ![]()
Exemple : On cherche la limite en ![]() de
de 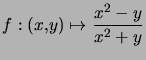
Cette fonction est définie et continue sur ![]() par application des théorèmes élémentaires.
par application des théorèmes élémentaires.
On calcule 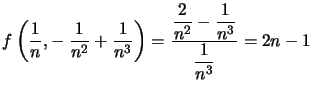 qui n'a pas de limite à l'infini, ce qui prouve que
qui n'a pas de limite à l'infini, ce qui prouve que ![]() n'a pas de limite en
n'a pas de limite en ![]()
Théorème : ![]() ,
, ![]() ,
, ![]() une partie fermée et bornée, alors
une partie fermée et bornée, alors ![]() est une partie bornée de
est une partie bornée de ![]() et les bornes sont atteintes.
et les bornes sont atteintes.
La démonstration est admise.