Chapitre 7 : Intégrale Simple, ou de Riemann

1 Intégration d'une fonction continue par morceaux sur $ \left[a,b\right] $

Sous-sections

1 Intégration d'une fonction continue par morceaux sur $ \left[a,b\right] $

1.1 Application continue par morceaux sur $ \left[a,b\right] $

Définition :   $ f$ définie sur $ \left[a,b\right] $, à valeur dans $ \mathbb{K}$$ \left( \mathbb{R}\text{ ou }\mathbb{C}\right) $.$ f$ est continue par morceaux sur $ \left[a,b\right] $\begin{displaymath}\Leftrightarrow\left\{ \begin{array}[c]{l} \text{il existe ... ...a_{i}\right[ }}}\text{ la prolong\'{e}e} \end{array} \right. \end{displaymath}

Définition :     On dit qu'une fonction est intégrable sur $ \left[ a,b\right] \Leftrightarrow$ cette fonction est continue par morceaux sur $ \left[a,b\right] $

1.2 Intégrale d'une fonction continue par morceaux

Théorème : (de Darboux)   Toute application continue sur un intervalle admet une primitive de classe$ \mathcal{C}^{1}$ sur cet intervalle.

Ce théorème est admis.

Définition :   $ f$ continue sur $ \left[a,b\right] $, à valeur dans $ \mathbb{K}$$ \left( \mathbb{R}\text{ ou }\mathbb{C}\right) $. $ F$ une primitive de $ f$, on appelle intégrale de $ f$ sur $ \left[a,b\right] $ :$ \displaystyle\int_{a}^{b}f\left( t\right) dt=F\left( b\right) -F\left( a\right) $

Remarque :   Il n'est pas nécessaire d'avoir $ a<b$, et on a immédiatement :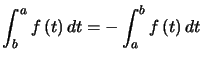$ \displaystyle\int_{b}^{a}f\left( t\right) dt=-\displaystyle\int_{a}^{b}f\left( t\right) dt$

Définition :   $ f$ continue par morceaux sur $ \left[a,b\right] $, à valeur dans$ \mathbb{K}$ $ \left( \mathbb{R}\text{ ou }\mathbb{C}\right) $. $ F_{i}$ une primitive de $ f_{i}$ sur $ \left[ a_{i-1},a_{i}\right] $, on appelle intégrale de $ f$ sur $ \left[a,b\right] $ :

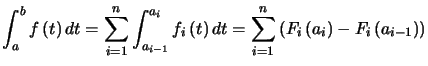
$\displaystyle \int_{a}^{b}f\left( t\right) dt=\sum\limits_{i=1}^{n}\int_{a_{i-1... ...{i=1}^{n}\left( F_{i}\left( a_{i}\right) -F_{i}\left( a_{i-1}\right) \right) $

1.3 Calcul approché d'intégrales et sommes de Riemann

On va faire un calcul approché de la valeur d'une intégrale de $ f$ sur$ \left[a,b\right] $ en divisant l'intervalle $ \left[a,b\right] $ en $ n$ parties égales.
Les bornes de ces parties sont donc 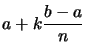$ a+k\dfrac{b-a}{n}$ pour $ k\in\left\{ 0, 1,\ldots, n\right\} $.
Sur chacun de ces intervalles de largeur $ \dfrac{b-a}{n}$ : $ \left[ a+\left( k-1\right) \dfrac{b-a} {n}, a+k\dfrac{b-a}{n}\right] $, définis pour $ k \in\left\{1, 2,\ldots, n\right\} $, on approxime la fonction par la valeur à une de ses deux bornes. Ce qui donne :

Théorème :   f continue sur $ \left[a,b\right] $

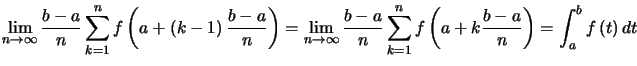
$\displaystyle \lim_{n\rightarrow\infty}\dfrac{b-a}{n}\sum_{k=1}^{n}f\left( a+\l... ...m_{k=1}^{n}f\left( a+k\dfrac{b-a}{n}\right) =\int_{a}^{b}f\left( t\right) dt $

Si de plus $ f$ est monotone, une figure montre facilement que l'une des deux sommes est un majorant, l'autre un minorant de l'intégrale.
Enfin, quand$ \left[ a,b\right] =\left[ 0,1\right] $, on obtient des sommes particulières appelées sommes de Riemann :

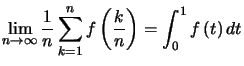
Théorème :   f continue sur $ \left[ 0,1\right] $, alors :$ \displaystyle\lim_{n\rightarrow\infty}\dfrac{1}{n}\displaystyle\sum_{k=1}^{n}f\left( \dfrac{k} {n}\right) =\displaystyle\int_{0}^{1}f\left( t\right) dt $

Ces théorèmes sont aussi applicables si les fonctions sont continues par morceaux sur l'intervalle $ \left[a,b\right] $

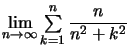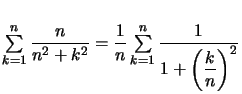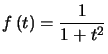Exemple :   Cherchons $ \lim\limits_{n\rightarrow\infty}\sum\limits_{k=1}^{n}\dfrac {n}{n^{2}+k^{2}}$ On écrit : $ \sum\limits_{k=1}^{n}\dfrac{n}{n^{2}+k^{2}}=\dfrac{1}{n}\sum\limits_{k=1} ^{n}\dfrac{1}{1+\left( \dfrac{k}{n}\right) ^{2}}$ et on reconnait une somme de Riemann pour la fonction $ f$ définie par $ f\left( t\right) =\dfrac {1}{1+t^{2}}$ sur $ \left[ 0,1\right] .$
On a bien une fonction continue sur$ \left[ 0,1\right] .$
La somme converge donc vers $ \displaystyle\int_{0}^{1}\dfrac{1}{1+t^{2}}\,dt=\dfrac{\pi}{4}.$

1.4 Propriétés

Théorème : (Linéarité)   $ f,g:\left[ a,b\right] \rightarrow\mathbb{K}$, intégrables sur $ \left[a,b\right] $, $ \lambda\in\mathbb{K}$, alors

$\displaystyle \displaystyle\int_{a}^{b}\lambda$ $\displaystyle f\left( t\right) dt$

$\displaystyle =\lambda\displaystyle\int_{a} ^{b}f\left( t\right) dt$

   

$\displaystyle \displaystyle\int_{a}^{b}\left( f+g\right) \left( t\right) dt$

$\displaystyle =\displaystyle\int_{a}^{b}f\left( t\right) dt+\displaystyle\int_{a}^{b}g\left( t\right) dt$

   


Théorème : (Conjugaison)   $ f:\left[ a,b\right] \rightarrow\mathbb{C}$, intégrable sur $ \left[a,b\right] $, alors

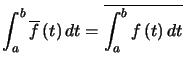
$\displaystyle \int_{a}^{b}\overline{f}\left( t\right) dt=\overline{\int_{a}^{b}f\left( t\right) dt} $

Théorème : (Relation de Chasles)   $ f:\left[ a,b\right] \cup\left[ a,c\right] \cup\left[ c,b\right] \rightarrow\mathbb{K}$, intégrable, alors

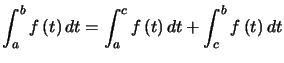
$\displaystyle \int_{a}^{b}f\left( t\right) dt=\int_{a}^{c}f\left( t\right) dt+\int _{c}^{b}f\left( t\right) dt $

Preuve. Ces théorèmes se montrent facilement en prenant $ F$ et $ G$ des primitives de $ f$ et $ g$ et en remarquant que $ \overline{F}$ est une primitive de $ \overline{f}$. $ \qedsymbol$

Exemple :   Calculons $ \displaystyle\int_{0}^{1}\dfrac{dt}{t+i}$ qui est bien l'intégrale d'une fonction continue sur $ \left[ 0,1\right] .$
Attention, le logarithme n'est défini que sur $ \mathbb{R}_{+}^{\ast},$ ceci nous oblige à séparer la partie réelle et la partie imaginaire.$ \displaystyle\int_{0}^{1}\dfrac{dt}{t+i}=\displaystyle\int_{0}^{1}\dfrac{t-i}{... ...ft( t\right) \right] _{0}^{1}=\dfrac{1}{2}\ln\left( 2\right) -i\dfrac{\pi}{4}.$

1.5 Inégalités

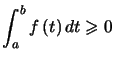
Théorème : (Croissance)   $ f:\left[ a,b\right] \rightarrow\mathbb{R}$, intégrable sur$ \left[a,b\right] $, positive sur $ \left[a,b\right] $, $ a<b$, alors :$ \displaystyle\int_{a}^{b}f\left( t\right) dt\geqslant0 $

Preuve. Sur chaque $ \left[ a_{i-1},a_{i}\right] ,F_{i}$ est croissante car de dérivée positive, d'où le résultat. $ \qedsymbol$

Théorème : (des 3 conditions)   $ f:\left[ a,b\right] \rightarrow\mathbb{R}: \left\{\begin{array}[c]{l} f \tex... ...y} \right\} \Rightarrow\forall t\in\left[ a,b\right] , f\left( t\right) =0 $

Preuve.$ F$ est croissante vérifiant $ F\left( b\right) =F\left( a\right) $, donc $ F$ est constante, de dérivée $ f$ nulle sur l'intervalle. $ \qedsymbol$

Théorème : (Majoration en valeur absolue)   $ a<b$,$ f:\left[ a,b\right] \rightarrow\mathbb{R}$, intégrable sur $ \left[a,b\right] $, alors $ \left\vert f\right\vert $ est intégrable sur $ \left[a,b\right] $, et :$ \left\vert \displaystyle\int_{a}^{b}f\left( t\right) dt\right\vert \leqslant\displaystyle\int_{a}^{b}\left\vert f\left( t\right) \right\vert dt $

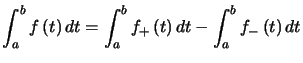Preuve. On définit $ f_{+}\left( t\right) =\max\left( f\left( t\right) ,0\right) $ et $ f_{-}\left( t\right) =\max\left( -f\left( t\right) ,0\right) $, deux fonctions positives, on a $ f\left( t\right) =f_{+}\left( t\right) -f_{-}\left( t\right) $ et$ \left\vert f\left( t\right) \right\vert =f_{+}\left( t\right) +f_{-}\left( t\right) $$ \displaystyle\int_{a}^{b}f\left( t\right) dt=\displaystyle\int_{a}^{b}f_{+}\left( t\right) dt-\displaystyle\int_{a}^{b}f_{-}\left( t\right) dt$ et $ \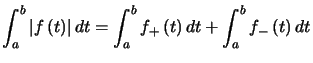displaystyle\int_{a}^{b}\left\vert f\left( t\right) \right\vert dt=\displays... ...}^{b}f_{+}\left( t\right) dt+\displaystyle\int_{a}^{b} f_{-}\left( t\right) dt$, ce qui assure le résultat car ces deux intégrales sont positives. $ \qedsymbol$

Théorème : (Majoration en module)   $ a<b$,$ f:\left[ a,b\right] \rightarrow\mathbb{C}$, intégrable sur $ \left[a,b\right] $, alors $ \left\vert f\right\vert $ est intégrable sur $ \left[a,b\right] $, et :$ \left\vert \displaystyle\int_{a}^{b}f\left( t\right) dt\right\vert \leqslant\displaystyle\int_{a}^{b}\left\vert f\left( t\right) \right\vert dt $

Preuve. Admis. $ \qedsymbol$

Théorème : (Inégalité de la moyenne)   $ a<b$$ f:\left[ a,b\right] \rightarrow\mathbb{C}$, intégrable sur $ \left[a,b\right] $, alors :$ \left\vert \displaystyle\int_{a}^{b}f\left( t\right) dt\right\vert \leqslant\l... ...le\sup\limits_{t\in\left[ a,b\right] }\left\vert f\left( t\right) \right\vert $

Preuve.$ \left\vert \displaystyle\int_{a}^{b}f\left( t\right) dt\right\vert \leqslant\d... ...) \sup\limits_{t\in\left[ a,b\right] }\left\vert f\left( t\right) \right\vert $ $ \qedsymbol$

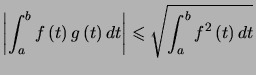
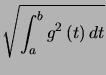
Théorème : (Inégalité de Cauchy-Schwarz)   $ a<b$$ f,g:\left[ a,b\right] \rightarrow\mathbb{R}$, intégrables sur $ \left[a,b\right] $, alors :$ \left\vert \displaystyle\int_{a}^{b}f\left( t\right) g\left( t\right) dt\right\vert \leqslant\sqrt{\displaystyle\int_{a}^{b}f^{2}\left( t\right) dt}$ $ \sqrt{\displaystyle\int _{a}^{b}g^{2}\left( t\right) dt} $

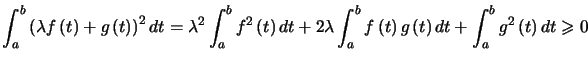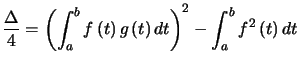
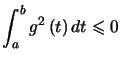Preuve.$ \displaystyle\int_{a}^{b}\left( \lambda f\left( t\right) +g\left( t\right) \ri... ...g\left( t\right) dt+\displaystyle\int_{a}^{b}g^{2}\left( t\right) dt\geqslant0$ pour tout $ \lambda$, d'où $ \dfrac{\Delta}{4}=\left( \displaystyle\int_{a}^{b}f\left( t\right) g\left( t\right) dt\right) ^{2}-\displaystyle\int_{a}^{b}f^{2}\left( t\right) dt$ $ \displaystyle\int_{a} ^{b}g^{2}\left( t\right) dt\leqslant0$ qui permet de conclure. $ \qedsymbol$


© Christophe Caignaert - Lycée Colbert - Tourcoing