Chapitre 7 : Intégrale Simple, ou de Riemann

2 Dérivation et Intégration

Sous-sections

2 Dérivation et Intégration

2.1 Intégration par parties

Théorème :   $ f$$ ,g:\left[ a,b\right] \rightarrow\mathbb{K}$, de classe $ \mathcal{C}^{1}$ sur $ \left[a,b\right] $, alors :$ \displaystyle\int_{a}^{b}f(t)g^{\prime}(t)\,dt= \left[ \rule{0 pt}{2.7 ex}f(t)g(t)\right] _{a}^{b}-\displaystyle\int_{a} ^{b}f^{\prime}(t)g(t)\,dt $

Preuve.$ f\times g$ est une primitive de $ f^{\prime}\times g+f\times g^{\prime}$ $ \qedsymbol$

Exemple :   Calculons 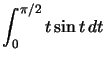$ \displaystyle\int_{0}^{\pi/2}t\sin t\,dt$ qui est bien l'intégrale d'une fonction continue sur $ \left[ 0,\dfrac{\pi}{2}\right] .$
On va intégrer par parties en dérivant le $ t$ et en intégrant le$ \sin t$
On obtient facilement : \begin{displaymath}\left\{ \begin{array}[c]{cc} f\left( t\right) =t & g^{\prim... ... t\right) =1 & g\left( t\right) =-\cos t \end{array} \right. \end{displaymath}
Ce qui donne : $ \displaystyle\int_{0}^{\pi/2}t\sin t\,dt=\left[ -t\cos t\right] _{0} ^{\pi/2}-\displaystyle\int_{0}^{\pi/2}-\cos t\,dt=0+\left[ \sin t\right] _{0}^{\pi/2}=1.$

2.2 Changement de variables

Théorème :   $ f$ continue sur $ \left[a,b\right] $, $ \varphi$ de classe $ \mathcal{C}^{1}$ sur $ \left[ \alpha,\beta\right] $, avec $ \varphi\left( \left[ \alpha ,\beta\right] \right) \subset\left[ a,b\right] $, alors

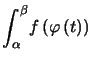
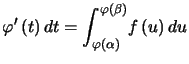
$\displaystyle {\displaystyle\int_{\alpha}^{\beta}} f\left( \varphi\left( t\right) \right)$    $\displaystyle \varphi^{\prime}\left( t\right) dt= {\displaystyle\int_{\varphi(\alpha)}^{\varphi(\beta)}} f\left( u\right) du $

Preuve. Si $ F$ est une primitive de $ f$, alors $ F\circ\varphi$ est une primitive de$ \left( f\circ\varphi\right) \times\varphi^{\prime}$, d'où

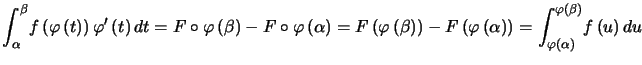
$\displaystyle {\displaystyle\int_{\alpha}^{\beta}} f\left( \varphi\left( t\rig... ... {\displaystyle\int_{\varphi(\alpha)}^{\varphi(\beta)}} f\left( u\right) du $

$ \qedsymbol$

Exemple :   Calculons 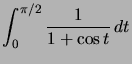$ \displaystyle\int_{0}^{\pi/2}\dfrac{1}{1+\cos t}\,dt$ qui est bien l'intégrale d'une fonction continue sur $ \left[ 0,\dfrac{\pi}{2}\right] .$
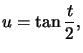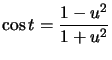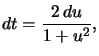Comme on le verra dans la suite, on pose $ u=\tan\dfrac{t}{2},$ ce qui donne$ \cos t=\dfrac{1-u^{2}}{1+u^{2}}$ et $ dt=\dfrac{2\,du}{1+u^{2}},$ on n'oublie pas de changer les bornes et on obtient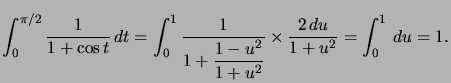 $ \displaystyle\int_{0}^{\pi/2}\dfrac{1}{1+\cos t}\,dt=\displaystyle\int_{0}^{1... ...{2}}{1+u^{2}}} \times\dfrac{2\,du}{1+u^{2} }=\displaystyle\int_{0}^{1}\,du=1.$
Les calculs ne s'arrangeront pas toujours ausssi bien !

2.3 Inégalité des accroissements finis

Théorème :   $ f:\left[ a,b\right] \rightarrow\mathbb{K}$, de classe $ \mathcal{C}^{1}$ sur$ \left[ a,b\right] ,a<b$ et $ k$ tel que $ \sup\limits_{t\in\left[ a,b\right] }\left\vert f^{\prime}\left( t\right) \right\vert \leqslant k$, alors :

$\displaystyle \left\vert f\left( b\right) -f\left( a\right) \right\vert \leqslant k\left( b-a\right) $

Preuve. Appliquer l'inégalité de la moyenne à $ f^{\prime}$. $ \qedsymbol$

2.4 Formules de Taylor

Les formules de Taylor sont toujours de la forme :

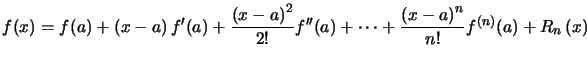
$\displaystyle f(x)=f(a)+\left( x-a\right) f^{\prime}(a)+\dfrac{\left( x-a\right... ...a)+\cdots+\dfrac{\left( x-a\right) ^{n}}{n!} f^{(n)}(a)+R_{n}\left( x\right) $

Le problème est alors de déterminer une valeur de $ R_{n}\left( x\right) $, un majorant de $ \left\vert R_{n}\left( x\right) \right\vert $ ou un ordre de grandeur d'un tel majorant.

2.4.1 Formule de Taylor avec reste intégral

Théorème :   Si $ f$ est de classe $ \mathcal{C}^{n+1}$ sur l'intervalle $ \left[ a,x\right] $

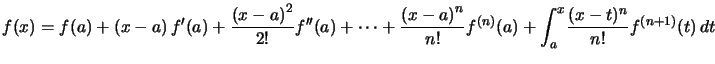
$\displaystyle f(x)=f(a)+\left( x-a\right) f^{\prime}(a)+\dfrac{\left( x-a\right... ...{(n)}(a)+ {\displaystyle\int_{a}^{x}} \dfrac{(x-t)^{n}}{n!}f^{(n+1)}(t)\,dt $

Preuve. Pour 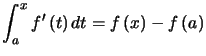$ n=0$, $ \displaystyle\int_{a}^{x}f^{\prime}\left( t\right) dt=f\left( x\right) -f\left( a\right) $ permet de conclure. On amorce donc une récurrence.
On admet le résultat au rang $ n$, une simple intégration par parties sur le reste donne :

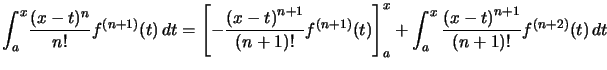
$\displaystyle {\displaystyle\int_{a}^{x}} \dfrac{(x-t)^{n}}{n!}f^{(n+1)}(t)\,d... ...a}^{x} \dfrac{\left( x-t\right) ^{n+1}}{\left( n+1\right) !}f^{(n+2)}(t)\,dt $

qui fournit immédiatement le résultat au rang $ n+1$. $ \qedsymbol$

2.4.2 Inégalité de Taylor-Lagrange

Théorème :   Si $ f$ est de classe $ \mathcal{C}^{n+1}$ sur l'intervalle $ \left[ a,x\right] $

$\displaystyle \left\vert f(x)-\left( f(a)+\sum_{k=1}^{n}\dfrac{\left( x-a\right... ...+1\right) !}\sup_{t\in\left[ a,x\right] }\left\vert f^{(n+1)} (t)\right\vert $

Preuve. On majore simplement l'intégrale dans la formule de Taylor avec reste intégral.
Le mieux est d'étudier 2 cas selon que $ x\geqslant a$ ou$ x\leqslant a$. $ \qedsymbol$

2.4.3 Formule de Taylor-Young

Théorème :   Si $ f$ est $ n$ fois dérivable au voisinage de $ a$,

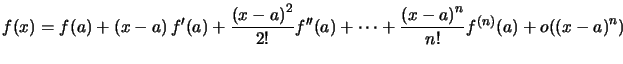
$\displaystyle f(x)=f(a)+\left( x-a\right) f^{\prime}(a)+\dfrac{\left( x-a\right... ...dots+\dfrac{\left( x-a\right) ^{n}}{n!} f^{(n)}(a)+o(\left( x-a\right) ^{n}) $

avec 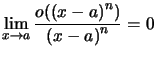$ \lim\limits_{x\rightarrow a}\dfrac{o(\left( x-a\right) ^{n})}{\left( x-a\right) ^{n}}=0$

Preuve. On le montre en supposant que $ f$ est de classe $ \mathcal{C}^{n+1}$ au voisinage de $ a$. L'inégalité de Taylor-Lagrange donne, en appelant$ M$ un majorant de $ \left\vert f^{(n+1)}(t)\right\vert $ sur un intervalle, voisinage de $ a$,

$\displaystyle \left\vert f(x)-\left( f(a)+\sum_{k=1}^{n}\dfrac{\left( x-a\right... ...x-a\right\vert ^{n} \dfrac{\left\vert x-a\right\vert M}{\left( n+1\right) !} $

Or $ \lim\limits_{x\rightarrow a}\dfrac{\left\vert x-a\right\vert M}{\left( n+1\right) !}=0$ assure le résultat. $ \qedsymbol$

2.5 Intégration et étude locale

Théorème :   $ f,g:I\rightarrow\mathbb{R}$, intégrables sur $ I$, $ a\in I$, $ g$ de signe constant à gauche et à droite de $ a$, alors

$\displaystyle f\left( x\right)$

$\displaystyle \underset{a}{=}o\left( g\left( x\right) \right) \Rightarrow\disp... ...) dt\underset{a}{=}o\left( \displaystyle\int_{a}^{x}g\left( t\right) dt\right)$

   

$\displaystyle f\left( x\right)$

$\displaystyle \underset{a}{\sim} g\left( x\right) \Rightarrow\displaystyle\int... ...left( t\right) dt\underset{a}{\sim}\displaystyle\int_{a}^{x}g\left( t\right) dt$

   



© Christophe Caignaert - Lycée Colbert - Tourcoing