Chapitre 7 : Intégrale Simple, ou de Riemann

3 Intégrales dépendant d'un paramètre

Sous-sections

3 Intégrales dépendant d'un paramètre

Il y a d'abord 2 théorèmes quand la fonction dépend d'un paramètre.
Ces 2 théorèmes vont être admis.
Il s'agit d'étudier la continuité et la classe $\mathcal{C}^{1}$ de $F:x\mapsto\displaystyle\int_{a}^{b}f\left( x,t\right) dt$ .
On a ensuite un théorème élémentaire quand les bornes dépendent d'un paramètre.
On a rapproché ces différents cas pour effectivement éviter les confusions.

3.1 Continuité

Théorème : (Continuité) $\begin{displaymath}f:\left\{ \begin{array}[c]{rcl} I\times\left[ a,b\right] & ... ...\mathbb{R}\\ (x,t) & \mapsto & f(x,t) \end{array} \right\} \end{displaymath}$ avec continue sur $I\times\left[ a,b\right]$ , un intervalle non vide et non réduit à un point.
alors définie par $F(x)=\displaystyle\int_{a}^{b}f(x,t)\,dt$ est continue sur I

Exemple : Soit définie par $F\left( x\right) =\displaystyle\int_{0}^{1}\dfrac{dt} {t^{2}+x^{2}}$ dont on va montrer qu'elle est continue sur $\mathbb{R} _{+}^{\ast}.$
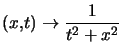$\left( x,t\right) \rightarrow\dfrac{1}{t^{2}+x^{2}}$ est bien continue sur $\mathbb{R}_{+}^{\ast}\times\left[ 0,1\right]$ comme fonction de 2 variables, ce qui prouve imméditement le résultat !

3.2 Classe $\mathcal{C}^{1}$

Théorème : (Classe $\mathcal{C}^{1}$ ) $\begin{displaymath}f:\left\{ \begin{array}[c]{rcl} I\times\left[ a,b\right] & ... ...\mathbb{R}\\ (x,t) & \mapsto & f(x,t) \end{array} \right\} \end{displaymath}$ avec continue sur $I\times\left[ a,b\right]$ , un intervalle non vide et non réduit à un point.
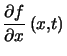Si, de plus, admet une dérivée partielle $\dfrac{\partial f}{\partial x}\left( x,t\right)$ , continue sur $I\times\left[ a,b\right]$ , alors est de classe $\mathcal{C}^{1}$ sur , et $F^{\prime }(x)=\displaystyle\int_{a}^{b}\dfrac{\partial f}{\partial x}(x,t)\,dt$

Exemple : On reprend l'exemple précédent avec définie par $F\left( x\right) =\displaystyle\int_{0}^{1}\dfrac{dt} {t^{2}+x^{2}}$ dont on va montrer maintenant qu'elle est de classe $\mathcal{C}^{1}$ sur $\mathbb{R} _{+}^{\ast}.$
On ne remontre pas la continuité déjà étudiée.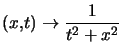 $\left( x,t\right) \rightarrow\dfrac{1}{t^{2}+x^{2}}$ admet une dérivée partielle par rapport à qui est $\dfrac{-2x}{\left( t^{2}+x^{2}\right) ^{2}}$ continue sur $\mathbb{R}_{+}^{\ast}\times\left[ 0,1\right]$ comme fonction de 2 variables, ce qui prouve imméditement que est de classe $\mathcal{C}^{1}$ sur $\mathbb{R} _{+}^{\ast}.$
De plus, toujours sur $\mathbb{R}_{+}^{\ast},$ $F^{\prime}\left( x\right) =\displaystyle\int_{0}^{1}\dfrac{-2x}{\left( t^{2}+x^{2}\right) ^{2}}\,dt$

3.3 Bornes dépendant d'un paramètre

Théorème : de classe $\mathcal{C}^{1}$ sur I, avec $a\left( I\right) \subset J$ et $b\left( I\right) \subset J$ , de plus est continue sur , alors $F:x\mapsto\displaystyle\int_{a\left( x\right) }^{b\left( x\right) }f\left( t\right) dt$ est de classe $\mathcal{C}^{1}$ sur , et : $F^{\prime}(x)=f\left( b\left( x\right) \right) b^{\prime}\left( x\right) -f\left( a\left( x\right) \right) a^{\prime}\left( x\right)$

Preuve. On appelle une primitive de , $F\left( x\right) =\displaystyle\int_{a\left( x\right) }^{b\left( x\right) }f\... ...\right) dt=g\left( b\left( x\right) \right) -g\left( a\left( x\right) \right)$ ce qui prouve que est de classe $\mathcal{C}^{1}$ sur , et $F^{\prime}(x)=f\left( b\left( x\right) \right) b^{\prime}\left( x\right) -f\left( a\left( x\right) \right) a^{\prime}\left( x\right)$ par simple dérivation de fonctions composées. $\qedsymbol$