Chapitre 8 : Intégrale généralisée

2 Intégrale des fonctions positives

Sous-sections

2 Intégrale des fonctions positives

Ce sont bien sûr des fonctions à valeurs réelles.

2.1 Critère de comparaison

Théorème :   $ \forall t\in\left[ a,b\right[ ,\quad0\leqslant f(t)\leqslant g(t)$

$\displaystyle \displaystyle\int_{a}^{b}g(t)\,dt$ converge 

$\displaystyle \Rightarrow\displaystyle\int_{a}^{b}f(t)\,dt$ converge

   

$\displaystyle \displaystyle\int_{a}^{b}f(t)\,dt$ diverge 

$\displaystyle \Rightarrow\displaystyle\int_{a}^{b}g(t)\,dt$ diverge

   


Théorème :   $ \forall t\in\left[ a,+\infty\right[ ,\quad0\leqslant f(t)\leqslant g(t)$

$\displaystyle \displaystyle\int_{a}^{+\infty}g(t)\,dt$ converge 

$\displaystyle \Rightarrow\displaystyle\int_{a}^{+\infty }f(t)\,dt$ converge

   

$\displaystyle \displaystyle\int_{a}^{+\infty}f(t)\,dt$ diverge 

$\displaystyle \Rightarrow\displaystyle\int_{a}^{+\infty }g(t)\,dt$ diverge

   


Preuve. A chaque fois, seule la première assertion est à montrer.
Soit $ F$ et $ G$ les primitives de $ f$ et $ g$ qui s'annulent en $ a$.
On a $ G$ qui est croissante majorée car l'intégrale de $ g$ converge.
D'autre part, en tout point $ t$ de $ I$, $ F\left( t\right) \leqslant G\left( t\right) $ et $ F$ est aussi croissante.
Ceci prouve que $ F$ est croissante majorée et donc converge.
.Enfin, l'intégrale de $ f$ converge sur $ I$. $ \qedsymbol$

Exemple :   On va déterminer la convergence de $ \displaystyle\int_{0}^{+\infty}\dfrac{\sin^{2} t}{1+t^{2}}\,dt.$ La fonction $ t\rightarrow\dfrac{\sin^{2}t}{1+t^{2}}$ est continue, donc localement intégrable sur $ \left[ 0,+\infty\right[ .$
On a un problème de convergence, ou une singularité, en $ +\infty.$
Par ailleurs, elle est positive et on va montrer la convergence de l'intégrale en utilisant le critère de comparaison : $ \forall t\in\left[ 0,+\infty\right[ ,$ $ 0\leqslant\dfrac{\sin^{2}t}{1+t^{2} }\leqslant\dfrac{1}{1+t^{2}}.$ Or $ \displaystyle\int_{0}^{+\infty}\dfrac{1}{1+t^{2}}\,dt$ converge par existence d'une limite finie à la primitive $ \arctan t$ en $ +\infty.$
Ceci prouve que 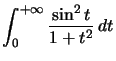$ \displaystyle\int_{0}^{+\infty}\dfrac{\sin^{2}t}{1+t^{2}}\,dt$ converge.

2.2 Critère d'équivalence

Théorème :   \begin{displaymath}\left. \begin{array}[c]{r} f(t)\underset{b^-}{\sim} g(t)\\ ... ...d{array} \right\} \Rightarrow\displaystyle\int_{a}^{b}f(t)\,dt\end{displaymath} et $ \displaystyle\int_{a}^{b}g(t)\,dt$ sont de même nature.

Théorème :   \begin{displaymath}\left. \begin{array}[c]{r} f(t)\underset{+\infty}{\sim} g(t... ...y} \right\} \Rightarrow\displaystyle\int_{a}^{+\infty}f(t)\,dt\end{displaymath} et $ \displaystyle\int_{a}^{+\infty}g(t)\,dt $ sont de même nature.

Preuve. Compte tenu de l'équivalence,
il existe $ a^{\prime}$ tel que sur $ \left[ a^{\prime},b\right[ $ $ \left( \text{ou sur }\left[ a^{\prime},+\infty\right[ \right) $, on a $ \frac{1} {2}g\left( t\right) \leqslant f\left( t\right) \leqslant2g\left( t\right) $.
Le caractère local de la convergence d'une intégrale, le critère de comparaison et la linéarité fournissent le résultat. $ \qedsymbol$

Exemple :   On va déterminer la convergence de $ \displaystyle\int_{0}^{1}\dfrac{\sin\sqrt{t}}{t}\,dt.$
La fonction $ t\rightarrow\dfrac{\sin\sqrt{t}}{t}$ est continue, donc localement intégrable sur $ \left] 0,1\right] .$
On a un problème de convergence, ou une singularité, en $ 0.$
Par ailleurs, elle est positive et on va montrer la convergence de l'intégrale en utilisant le critère d'équivalence : $ \dfrac {\sin\sqrt{t}}{t}\underset{0}{\sim}\dfrac{1}{\sqrt{t}}.$
Or $ \displaystyle\int_{0} ^{1}\dfrac{dt}{\sqrt{t}}$ converge par existence d'une limite finie à la primitive $ 2\sqrt{t}$ en 0.
Ceci prouve que $ \displaystyle\int_{0}^{1}\dfrac{\sin\sqrt{t}}{t}\,dt$ converge.

2.3 Théorème des 3 conditions

Théorème :   \begin{displaymath}\left. \begin{array}[c]{r} \forall t\in\left[ a,b\right[ ,\... ...\right\} \Rightarrow\forall t\in\left[ a,b\right[ ,\quad f(t)=0\end{displaymath}

$ b$ peut être une borne finie ou $ +\infty,$ on a bien sûr le même théorème sur $ \left] a,b\right] ,$ que $ a$ soit fini ou $ -\infty.$
On utilise souvent ce théorème, par exemple quand on a un produit scalaire défini par une intégrale, pour montrer le caractère défini-positif de la forme quadratique.

© Christophe Caignaert - Lycée Colbert - Tourcoing