Définition : ![]() localement intégrable sur
localement intégrable sur ![]() , à valeur dans
, à valeur dans ![]() ,
,
on dit que l'intégrale de ![]() est absolument convergente
est absolument convergente ![]() l'intégrale de
l'intégrale de ![]() converge absolument.
converge absolument.
Exemple :  converge.
converge.
Théorème : ![]() localement intégrable sur
localement intégrable sur ![]() , dont l'intégrale converge absolument sur
, dont l'intégrale converge absolument sur ![]() ,
,
alors l'intégrale de ![]() converge sur
converge sur ![]() et :
et : 
Preuve. On va le montrer pour une fonction qui est à priori à valeurs complexes.
![]()
Définition : On dit que l'intégrale de ![]() est semi convergente sur
est semi convergente sur ![\begin{displaymath}I\Leftrightarrow\left\{
\begin{array}[c]{l}
\text{l'int\'{e...
...\right\vert \text{ sur }I\text{ diverge}
\end{array}
\right. \end{displaymath}](img111.png)
Exemple : 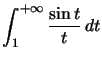 est semi convergente.
est semi convergente.
 , et
, et  converge absolument donc converge.
converge absolument donc converge.  , et
, et  converge absolument donc converge.
converge absolument donc converge.Remarque : Ceci n'est pas un théorème, il faut à chaque fois refaire la démonstration...
Il faut y observer qu'on travaille avec une fonction positive ou montrer la convergence absolue.
Exemple : On va déterminer la convergence de  La fonction
La fonction  est continue, donc localement intégrable sur
est continue, donc localement intégrable sur ![]()
On a un problème de convergence, ou une singularité, en 0 et en ![]()
En 0,  tend vers 0, d'où
tend vers 0, d'où  et ainsi, par comparaison,
et ainsi, par comparaison,  converge absolument donc converge.
converge absolument donc converge.
En ![]()
 tend vers 0, d'où
tend vers 0, d'où  et ainsi, par comparaison,
et ainsi, par comparaison,  converge absolument donc converge.
converge absolument donc converge.
Ceci prouve que  converge.
converge.
Théorème : Si ![]() est de signe constant sur
est de signe constant sur ![]() , alors :
, alors :  et
et  sont de même nature.
sont de même nature.
La convergence de l'intégrale équivaut à sa convergence absolue.
Preuve. ![]() ou
ou ![]() est positive, l'une des deux est :
est positive, l'une des deux est : ![]() .
.
La linéarité des intégrales convergentes permet de conclure. ![]()
Remarque : Quand on utilise ce théorème, on écrit clairement que dans le cas d'une fonction de signe constant, la convergence de son intégrale équivaut à sa convergence absolue.