Chapitre 8 : Intégrale généralisée

4 Intégration et Dérivation

Sous-sections

4 Intégration et Dérivation

4.1 Intégration par parties

Théorème : $\begin{displaymath}\left. \begin{array}[c]{r} u\text{ et }v\text{ de classe }\... ...ht\} \Rightarrow\displaystyle\int_{a}^{b}u(t)v^{\prime}(t)\,dt\end{displaymath}$ et $\displaystyle\int_{a} ^{b}u^{\prime}(t)v(t)\,dt$ sont de même nature
et si elles convergent : $\displaystyle\int_{a}^{b}u(t)v^{\prime}(t)\,dt =\left[ \rule{0 pt}{2.7 ex} u(t)v(t)\right] _{a}^{b^{-}}-\displaystyle\int _{a}^{b}u^{\prime}(t)v(t)\,dt$

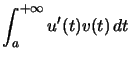Théorème : $\begin{displaymath}\left. \begin{array}[c]{r} u\text{ et }v\text{ de classe }\... ...\Rightarrow\displaystyle\int_{a}^{+\infty}u(t)v^{\prime}(t)\,dt\end{displaymath}$ et $\displaystyle\int _{a}^{+\infty}u^{\prime}(t)v(t)\,dt$ sont de même nature
et si elles convergent : $\displaystyle\int_{a}^{+\infty}u(t)v^{\prime}(t)\,dt= \left[ \rule{0 pt}{2.7 ... ...\right] _{a}^{+\infty }-\displaystyle\int_{a}^{+\infty}u^{\prime}(t)v(t)\,dt$

Remarque : Ces théorèmes sont à utiliser avec soin.
La rédaction se fait toujours en deux temps

une partie sur la nature des intégrales et
en cas de convergence, l'égalité proprement dite.

Preuve. On le montre dans le premier cas, la démonstration est la même dans les autres cas.
On a toujours : $\displaystyle\int_{a}^{x}u(t)v^{\prime}(t)\,dt= \left[ \rule{0 pt}{2.7 ex}u(t)v(t)\right] _{a}^{x}-\displaystyle\int_{a} ^{x}u^{\prime}(t)v(t)\,dt$ Si $u\left( x\right) v\left( x\right)$ a une limite finie quand $x\rightarrow b^{-}$ , les deux intégrales ont toutes les deux une limite finie ou toutes les deux pas de limite finie.
Elles sont donc de même nature.
Dans le cas où elles convergent, en passant à la limite quand $x\rightarrow b^{-}$ , on obtient l'égalité annoncée. $\qedsymbol$

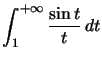Exemple : $\displaystyle\int_{1}^{+\infty}\dfrac{\sin t}{t}\,dt$ converge. En effet $\dfrac{\sin t}{t}$ est continue sur $\left[ 1,+\infty\right[$ , donc localement intégrable sur $\left[ 1,+\infty\right[$
C'est une intégrale généralisée en $+\infty$ .
Montrons sa convergence grace au théorème d'intégration par parties.
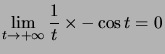On pose $u\left( t\right) =\dfrac{1}{t}$ et $v\left( t\right) =-\cos t$ , on a : $\lim\limits_{t\rightarrow+\infty}\dfrac{1}{t}\times-\cos t=0$ qui est une limite finie,
ce qui prouve que 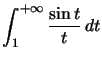$\displaystyle\int_{1}^{+\infty}\dfrac{\sin t}{t}\,dt$ et $\displaystyle\int _{1}^{+\infty}\dfrac{\cos t}{t^{2}}\,dt$ sont de même nature.
Or 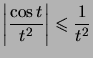$\left\vert \dfrac{\cos t}{t^{2}}\right\vert \leqslant\dfrac{1}{t^{2}}$ et $\displaystyle\int_{1}^{+\infty}\dfrac{1}{t^{2}}\,dt$ converge par Riemann.
Donc, par Riemann, comparaison, convergence absolue et intégration par parties, 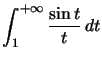$\displaystyle\int_{1}^{+\infty}\dfrac{\sin t}{t}\,dt$ converge.

4.2 Changement de variable

Théorème : $\beta$ étant une borne finie ou $+\infty$ , $\begin{displaymath}\left. \begin{array}[c]{r} f\text{ continue sur }I\\ \var... ...rphi\left( t\right) \right) \varphi^{\prime}\left( t\right) dt\end{displaymath}$ et ${\displaystyle\int_{\varphi(\alpha)}^{\varphi(\beta)}} f\left( u\right) du$ sont de même nature
et si elles convergent : ${\displaystyle\int_{\alpha}^{\beta}} f\left( \varphi\left( t\right) \right) \... ... {\displaystyle\int_{\varphi(\alpha)}^{\varphi(\beta)}} f\left( u\right) du$

Remarque : Ce théorème est à utiliser avec soin.
La rédaction se fait toujours en deux temps

une partie sur la nature des intégrales et
en cas de convergence, l'égalité proprement dite.

Preuve. On a toujours : ${\displaystyle\int_{\alpha}^{x}} f\left( \varphi\left( t\right) \right) \varp... ... dt= {\displaystyle\int_{\varphi(\alpha)}^{\varphi(x)}} f\left( u\right) du$
Ce sont deux fonctions continues de et égales.
Elles ont donc toutes les deux une limite finie ou pas de limite finie quand $x\rightarrow\beta$ .
Dans le cas où elles ont une limite finie, par passage à la limite, on a l'égalité annoncée. $\qedsymbol$

Remarque : Un changement de variable peut transformer une intégrale simple en intégrale généralisée et vice-versa.
Dans ce cas, à condition de le remarquer, il n'y a pas de problème d'intégrabilité.
Regardons par exemple 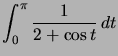$\displaystyle\int_{0}^{\pi}\dfrac{1}{2+\cos t}\,dt$ pour lequel $u=\tan\frac{t}{2}$ donne $\displaystyle\int_{0}^{+\infty}\ldots du$ .

Exemple : On va déterminer la convergence de $\displaystyle\int_{0}^{+\infty}\sin\left( e^{t}\right) dt.$
La fonction $t\rightarrow\sin\left( e^{t}\right)$ est continue, donc localement intégrable sur $\left[ 0,+\infty\right[ .$ On a un problème de convergence, ou une singularité, en $+\infty.$
On va montrer la convergence de cette intégrale au moyen d'un changement de variable : on pose $u=e^{t}$ qui est bien monotone de classe $\mathcal{C}^{1},$ $\sin\left( e^{t}\right) \,dt=\dfrac{\sin u}{u}\,du$ et ainsi $\displaystyle\int_{0}^{+\infty}\sin\left( e^{t}\right) dt$ est de même nature que $\displaystyle\int_{1}^{+\infty}\dfrac{\sin u}{u}\,du.$
Par ailleurs, on a montré que $\displaystyle\int_{1}^{+\infty}\dfrac{\sin u}{u}\,du$ converge et donc $\displaystyle\int_{0}^{+\infty}\sin\left( e^{t}\right) dt$ converge.