Chapitre 9 : Séries numériques

3 Séries à termes positifs

Sous-sections

3 Séries à termes positifs

3.1 Séries à termes positifs

Définition : On dit qu'une série $\displaystyle\sum u_{n}$ est une série à termes positifs $\Leftrightarrow\forall n\in\mathbb{N}$ , $u_{n}\geqslant0$ .

Définition : On dit qu'une série $\displaystyle\sum u_{n}$ est une série à termes positifs à partir d'un certain rang

$\displaystyle \Leftrightarrow\exists N\in\mathbb{N},\forall n\geqslant N,u_{n}\geqslant0$

3.2 Critère de comparaison

Théorème : $\displaystyle\sum u_{n}$ et $\displaystyle\sum v_{n}$ deux séries positives à partir d'un certain rang , telles que

$\displaystyle \forall n\geqslant N, u_{n}\leqslant v_{n}$

Si $\displaystyle\sum v_{n}$ converge, alors $\displaystyle\sum u_{n}$ converge. Si $\displaystyle\sum u_{n}$ diverge, alors $\displaystyle\sum v_{n}$ diverge.

Preuve. Seule la première assertion est à montrer, l'autre est équivalente. On le montre pour les séries positives $\left( N=0\right)$ .
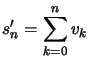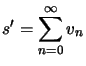On pose $s_{n}=\displaystyle\sum\limits_{k=0}^{n}u_{k}$ , $s_{n}^{\prime}=\displaystyle\sum \limits_{k=0}^{n}v_{k}$ et $s^{\prime}=\displaystyle\sum\limits_{n=0}^{\infty}v_{n}$ , on a $s_{n}\leqslant s_{n}^{\prime}$ .
Les suites $\left( s_{n}\right)$ et $\left( s_{n}^{\prime}\right)$ sont croissantes et la deuxième converge.
On a donc $s_{n}^{\prime}\leqslant s^{\prime}$ . Ce qui prouve que $\left( s_{n}\right)$ est croissante majorée et donc converge.
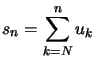Pour le cas de séries positives à partir du rang , on considère les sommes partielles $s_{n}=\displaystyle\sum\limits_{k=N}^{n}u_{k}$ ... $\qedsymbol$

Exemple : Etudions la convergence de 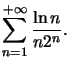$\displaystyle\sum\limits_{n=1}^{+\infty}\dfrac{\ln n}{n2^{n}}.$
C'est une série à termes positifs (ou plus simplement positive), on va pouvoir utiliser le critère de comparaison.
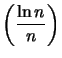A l'infini, $\dfrac{\ln n}{n}$ tend vers 0 et donc $\left( \dfrac{\ln n} {n}\right)$ est une suite bornée par
On a donc 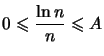$\forall n\in\mathbb{N}^{\ast},$ $0\leqslant\dfrac{\ln n}{n}\leqslant A$ ce qui donne 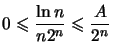$\forall n\in\mathbb{N}^{\ast},$ $0\leqslant\dfrac{\ln n}{n2^{n}} \leqslant\dfrac{A}{2^{n}}$ qui est le terme général d'une série géométrique de raison $\dfrac{1}{2},$ donc convergente.
Ceci prouve que 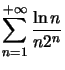$\displaystyle\sum\limits_{n=1}^{+\infty}\dfrac{\ln n}{n2^{n}}$ converge.

3.3 Critère d'équivalence

Théorème : $\displaystyle\sum u_{n}$ et $\displaystyle\sum v_{n}$ deux séries positives à partir d'un certain rang , telles que : $u_{n}\underset{+\infty}{\sim} v_{n}$
alors $\displaystyle\sum u_{n}$ et $\displaystyle\sum v_{n}$ sont de même nature.

Preuve. A partir d'un certain rang , on a $0\leqslant\frac{1}{2}u_{n}\leqslant v_{n}\leqslant2u_{n}$ .
Si $\displaystyle\sum u_{n}$ converge, $\displaystyle\sum 2u_{n}$ converge et donc $\displaystyle\sum v_{n}$ converge.
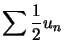Si $\displaystyle\sum v_{n}$ converge, $\displaystyle\sum\frac{1}{2}u_{n}$ converge et donc $\displaystyle\sum u_{n}$ converge. $\qedsymbol$

On peut remarquer que le critère d'équivalence est, par liné arité, applicable à des séries de signe constant à partir d'un certain rang.

Exemple : Etudions la convergence de 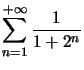$\displaystyle\sum\limits_{n=1}^{+\infty}\dfrac{1}{1+2^{n}}$ .
C'est une série à termes positifs (ou plus simplement positive), on va pouvoir utiliser le critère d'équivalence. $\dfrac{1}{1+2^{n}}\underset{+\infty}{\sim}\dfrac{1}{2^{n}}$ qui est le terme général d'une série géométrique de raison $\dfrac{1}{2},$ donc convergente.
Ceci prouve que 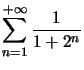$\displaystyle\sum\limits_{n=1}^{+\infty}\dfrac{1}{1+2^{n}}$ converge.

3.4 Comparaison à une intégrale impropre

Théorème : Soit une application positive et décroissante sur $\left[ a,+\infty\right[$ ,
alors la série $\displaystyle\sum f\left( n\right)$ et $\displaystyle\int_{a}^{+\infty}f\left( t\right) dt$ sont de même nature.
Et si elles convergent, 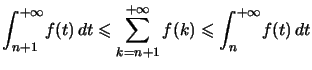${\displaystyle\int_{n+1}^{+\infty}} f(t)\,dt\leqslant\displaystyle\sum_{k=n+1}^{+\infty}f(k)\leqslant {\displaystyle\int_{n}^{+\infty}} f(t)\,dt$

Preuve. Remarquons d'abord que, comme 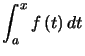$\displaystyle\int_{a}^{x}f\left( t\right) dt$ est croissante, $\displaystyle\int_{a}^{+\infty}f\left( t\right) dt$ converge $\Leftrightarrow$ la suite $\left( \displaystyle\int_{a}^{p}f\left( t\right) dt\right)$ converge.
On prendra pour la démonstration . Comme décroit sur $\left[ n,n+1\right]$ ,

$\displaystyle \forall x\in\left[ n,n+1\right] , f\left( n+1\right) \leqslant f\left( x\right) \leqslant f\left( n\right)$

et en intégrant, comme on peut le voir sur la figure ci-dessous : 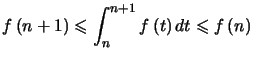$f\left( n+1\right) \leqslant\displaystyle\int_{n}^{n+1}f\left( t\right) dt\leqslant f\left( n\right)$ .

$\includegraphics[ width=4.5in ]{comparaison-serie-integrale}$

d'où en sommant 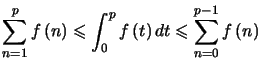$\displaystyle\sum\limits_{n=1}^{p}f\left( n\right) \leqslant\int_{0}^{p}f\left( t\right) dt\leqslant\displaystyle\sum\limits_{n=0}^{p-1}f\left( n\right)$ , ce qui assure le résultat. $\qedsymbol$

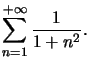
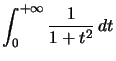Exemple : Etudions la convergence de $\displaystyle\sum\limits_{n=1}^{+\infty}\dfrac{1}{1+n^{2}}.$ définie par $f\left( t\right) =\dfrac{1}{1+t^{2}}$ est positive, décroissante sur $\left[ 0,+\infty\right[$ et $\displaystyle\int_{0}^{+\infty} \dfrac{1}{1+t^{2}}\,dt$ converge et est de même nature que la série étudiée.
Ceci prouve que 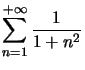$\displaystyle\sum\limits_{n=1}^{+\infty}\dfrac{1}{1+n^{2}}$ converge.

3.5 Règle de Riemann

Théorème : 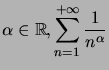$\alpha\in\mathbb{R},\displaystyle\sum\limits_{n=1}^{+\infty}\dfrac{1}{n^{\alpha}}$ converge $\Leftrightarrow$ $\alpha>1$ .

Ce sont les séries de Riemann.

Preuve. On compare cette série avec 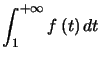$\displaystyle\int_{1}^{+\infty}f\left( t\right) dt$ et le résultat est immédiat. $\qedsymbol$

Ceci nous donne la règle de Riemann.

Théorème : 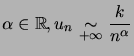$\alpha\in\mathbb{R}, u_{n}\underset{+\infty}{\sim}\dfrac{k}{n^{\alpha}}$ , alors : $\displaystyle\sum u_{n}$ converge $\Leftrightarrow\alpha>1$ .

Preuve. Il suffit d'utiliser le critère d'équivalence et le théorème précédent. $\qedsymbol$

3.6 Règle de d'Alembert

Théorème : $\displaystyle\sum u_{n}$ une série à termes positifs non nuls (à partir d'un certain rang) telle que : $\displaystyle\displaystyle\lim\limits_{n\rightarrow\infty}\dfrac{u_{n+1}}{u_{n}}=l$

si , $\displaystyle\sum u_{n}$ diverge grossièrement,
si , $\displaystyle\sum u_{n}$ converge,
et si , on ne peut pas conclure.

Remarque : Ce théorème est séduisant à priori, mais on tombe très souvent sur le cas douteux.
Il s'utilise souvent dans le cadre des séries entières qu'on étudiera dans quelques chapitres. Avec les séries numériques, il s'utilise principalement quand on se trouve en présence de factorielles ou de termes de nature géométrique du type : $a^{n}$ .

Preuve. Pour , la suite positive $\left( u_{n}\right)$ croit et ne tend donc pas vers 0. On a bien la divergence grossière.
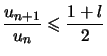Pour , à partir d'un certain rang $\dfrac{u_{n+1}}{u_{n}}\leqslant\dfrac{1+l}{2}$ .
et donc par récurrence très facile, pour $n\geqslant N$ , $u_{n}\leqslant\left( \dfrac{1+l}{2}\right) ^{n-N}u_{N}=\left( \dfrac {1+l}{2}\right) ^{n}\dfrac{u_{N}}{\left( \dfrac{1+l}{2}\right) ^{N}}$ .
Cette dernière série est géométrique, le théorème de comparaison entre séries positives fournit le résultat. $\qedsymbol$

Exemple : Etudions la convergence de 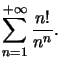$\displaystyle\sum\limits_{n=1}^{+\infty}\dfrac{n!}{n^{n}}.$
C'est une série à termes strictement positifs, on va pouvoir utiliser le critère de d'Alembert. $\dfrac{\dfrac{\left( n+1\right) !}{\left( n+1\right) ^{n+1}}}{\dfrac {n!}{n^{... ...left( 1+\dfrac{1}{n}\right) ^{n}}\underset{+\infty}{\rightarrow}\dfrac{1}{e}<1$
Ceci prouve que 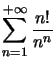$\displaystyle\sum\limits_{n=1}^{+\infty}\dfrac{n!}{n^{n}}$ converge.