Théorème : La limite ![]() , quand elle existe, est unique.
, quand elle existe, est unique.
Remarque : Cette définition est valable pour une suite réelle ou complexe.
Dans le cas d'une suite vectorielle, il suffit de remplacer ![]() par
par ![]() .
.
Théorème : L'ensemble des suites muni de la somme de deux suites et de la multiplication par un scalaire a une structure d'espace vectoriel sur ![]() .
.
Il en est de même de l'ensemble des suites convergentes.
Définition : ![]() est une sous-suite de
est une sous-suite de![]() strictement croissante telle que
strictement croissante telle que ![]()
Théorème : ![]() converge vers
converge vers ![]() toute sous-suite de
toute sous-suite de ![]() converge vers
converge vers ![]()
Si deux sous-suites ont des limites différentes ou si une sous-suite diverge, la suite diverge.
Théorème : Une suite convergente est bornée.
Théorème : Quand ![\begin{displaymath}n\rightarrow+\infty,\quad\left. \begin{array}[c]{r} u_{n}\r... ... \lambda\, u_{n}\rightarrow\lambda\, l \end{array} \right. \end{displaymath}](img346.png)
Théorème : On a ![]() et
et ![]() , alors
, alors ![\begin{displaymath}u_{n}\rightarrow l\Leftrightarrow\left\{ \begin{array}[c]{c}... ...}\\ \vdots\\ u_{pn}\rightarrow l_{p} \end{array} \right. \end{displaymath}](img349.png)
Définition : Deux suites sont équivalentes ![]() avec
avec ![]() .
.
En pratique, si à partir d'un certain rang ![]() , cela revient à
, cela revient à ![]() .
.
Théorème : La suite ![]() converge
converge ![]() La série
La série ![]() converge
converge
Théorème : Toute suite croissante majorée converge.
Théorème : Toute suite décroissante minorée converge.
Théorème : (suites adjacentes) ![\begin{displaymath}\left. \begin{array}[c]{r} (u_{n})\nearrow\\ (v_{n})\sear... ...n}-v_{n})\rightarrow0 \end{array} \right\} \Rightarrow(u_{n})\end{displaymath}](img356.png) et
et ![]() convergent vers la même limite
convergent vers la même limite
On a ![]() , et
, et ![]() et si
et si ![]() Il y a principalement deux méthodes distinctes.
Il y a principalement deux méthodes distinctes.
La première est la plus pratique, souvent on y est un peu guidé par l'énoncé.
La seconde est plus fastidieuse...
Il est basé sur l'inégalité des accroissements finis.
Si, sur un intervalle ![]() stable par
stable par ![]() ,
, ![]() un point fixe, et
un point fixe, et ![]() , on montre que
, on montre que ![]() et donc par récurrence immédiate, que
et donc par récurrence immédiate, que ![]() ce qui assure la convergence.
ce qui assure la convergence.
![]()
Il s'agit, comme dans toute « équation linéaire », d'ajouter une solution particulière du problème avec second membre à la solution générale du problème sans second membre.
![]() La solution est géométrique
La solution est géométrique 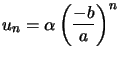
![]() Chercher une solution particulière sous forme de suite constante
Chercher une solution particulière sous forme de suite constante
![]() On calcule les solutions de l'équation caractéristique
On calcule les solutions de l'équation caractéristique ![]()
![]() Chercher une solution particulière
Chercher une solution particulière