Résumé de Cours de Sup et Spé T.S.I.

Deuxième Partie : Analyse

16 Dérivabilité

Sous-sections

16 Dérivabilité

Définition :   $ f$ est dérivable en $ a$ $ \Leftrightarrow\dfrac{f(x)-f(a)}{x-a} $ a une limite finie quand $ x$ tend vers $ a$.
C'est cette limite qu'on note $ f'(a)$.

Théorème :   $ f$ dérivable en $ a$ $ \Rightarrow$$ f$ est continue en $ a$.
La réciproque est fausse!

16.1 Sommes et produits de fonctions dérivables

Théorème :   $ f$ et $ g$ dérivables en un point ou sur un intervalle\begin{displaymath}\Rightarrow\left\{ \begin{array}[c]{l} (f+g)^{\prime}=f^{\p... ...rime}\times g-f\times g^{\prime}}{g^{2}} \end{array} \right.\end{displaymath}
En se plaçant pour cette dernière propriété en un point où $ g$ est non nulle.

Théorème :   Si $ f$ et $ g$ sont $ n$ fois dérivables $ \left( f\times g\right) ^{(n)}=\displaystyle\sum_{k=0}^{n}\,\mathcal{C}_{n}^{k}\,f^{(k)}\times g^{(n-k)}$
Ceci s'utilise surtout avec une des deux fonctions qui est un polynôme, une exponentielle ou une fonction trigonométrique.

16.2 Dérivée d'une fonction composée

Théorème :   $ \left( g\circ f\right) ^{\prime}=\left( g^{\prime}\circ f\right) \times f^{\prime}$ c'est à dire $ :\left( g\left( f\left( x\right) \right) \right) ^{\prime}=g^{\prime}\left( f\left( x\right) \right) \times f^{\prime}\left( x\right) $

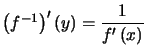Théorème :   En un point où $ f^{\prime}$ est non nulle: $ \left( f^{-1}\right) ^{\prime}=\dfrac{1}{f^{\prime}\circ f^{-1}}$ c'est à dire $ \left( f^{-1}\right) ^{\prime}\left( y\right) =\dfrac{1}{f^{\prime}\left( x\right) }$ avec les notations habituelles $ y=f(x)$.

16.3 Dérivée et prolongement par continuité

Pour étudier la dérivabilité d'une fonction en un point où elle a été prolongée par continuité, on peut

16.4 Théorème de Rolle et des Accroissements Finis, Formules de Taylor

Théorème :   (Rolle)$ f$ continue sur $ \left[ a,b\right] $, dérivable sur $ \left] a,b\right[ ,\quad f(a)=f(b) \Rightarrow\exists c\in\left] a,b\right[ $, tel que :$ f^{\prime}(c)=0$

Théorème :   (Egalité des accroissements finis)$ f$ continue sur $ \left[ a,b\right] $, dérivable sur $ \left] a,b\right[ ,\Rightarrow\exists c\in\left] a,b\right[ $, tel que $ f^{\prime }(c)=\dfrac{f(b)-f(a)}{b-a}$

Théorème : (Inégalité des accroissements finis)   $ f$ continue sur $ \left[ a,b\right] $, dérivable sur $ \left] a,b\right[ $, de dérivée bornée, $ \Rightarrow\left\vert \dfrac{f(b)-f(a)}{b-a}\right\vert \leqslant \displaystyle\sup_{c\in\left] a,b\right[ }\left\vert f^{\prime}(c)\right\vert $

On n'écrira ici que les formules de Taylor en 0 ou sur l'intervalle$ \left[ 0,x\right] $.
On peut se placer en un point $ a$ ou sur $ \left[ a,b\right] $, en adaptant les notations.

Théorème :   (Taylor-Young) Si $ f$ est $ n$-fois dérivable au voisinage de 0,

$\displaystyle f(x)=f(0)+xf^{\prime}(0)+\dfrac{x^{2}}{2!}f^{\prime\prime}(0)+\cdots +\dfrac{x^{n}}{n!}f^{(n)}(0)+o(x^{n})$   avec $\displaystyle \lim_{x\rightarrow 0}\dfrac{o(x^{n})}{x^{n}}=0 $

Théorème :   (Taylor avec reste intégral) Si $ f$ est de classe $ \mathcal{C}^{n+1}$ sur l'intervalle

$\displaystyle f(x)=f(0)+xf^{\prime}(0)+\dfrac{x^{2}}{2!}f^{\prime\prime}(0)+\cd... ...{(n)}(0)+ {\displaystyle\int_{0}^{x}} \dfrac{(x-t)^{n}}{n!}f^{(n+1)}(t)\,dt $

Théorème :   (Inégalité de Taylor-Lagrange) Si $ f$ est de classe $ \mathcal{C}^{n+1}$ sur l'intervalle

$\displaystyle \left\vert f(x)-\left( f(0)+xf^{\prime}(0)+\dfrac{x^{2}}{2!}f^{\p... ...n+1\right) !}\sup_{t\in\left[ 0,x\right] }\left\vert f^{(n+1)}(t)\right\vert $


16.5 Développements limités

On n'écrira ici que des développements limités en 0. on peut se placer en un point $ a$ en adaptant les notations.

Définition :   On dit que $ f$ admet un développement limité à l'ordre n en 0$ \Leftrightarrow$ il existe $ a_{0},\, a_{1},\ldots,\, a_{n}$ tels que $ f(x)=a_{0} +a_{1}x+\cdots+a_{n}x^{n}+o(x^{n})$

Remarque :   $ f$ admet un $ dl_{0}$ en 0 $ \Leftrightarrow$ $ f$ est continue en 0
$ f$ admet un $ dl_{1}$ en 0 $ \Leftrightarrow$ $ f$ est dérivable en 0. (mais on ne peut pas généraliser à un $ dl_{n}$...)

Théorème :   $ f$ est de classe $ \mathcal{C}^{n}$ en 0 $ \Rightarrow$ $ f$ admet un $ dl_{n}$ en 0, qui est le développement de Taylor!

16.6 Opérations sur les $ dl_{n}$

On agira toujours avec des développements au même ordre.


16.7 Fonctions usuelles

16.7.1 Exponentielle et Logarithme

La fonction exponentielle : $ x\rightarrow \exp(x)$ est définie sur $ \mathbb{R}$ ou sur $ \mathbb{C}$.
Elle vérifie la propriété fondamentale :     $ \exp(a+b)=\exp(a) \, \exp(b)$.
La fonction logarithme est la réciproque de la précédente et n'est définie que sur $ \mathbb{R}_+^*$.
Elle vérifie la propriété fondamentale :    $ \ln(a \, b)=\ln(a)+\ln(b)$.
Ces deux fonctions sont tracées sur la figure ci-dessous.

\includegraphics[

16.7.2 Fonction trigonométriques hyperboliques

Rappelons la relation fondamentale de la trigonométrie hyperbolique :    $ \mathrm{ch}^{2}\, a-\mathrm{sh}^{2}\, a=1$
Les deux fonctions $ x \rightarrow \mathrm{ch}(x)$ et $ x \rightarrow \mathrm{sh}(x)$ sont tracées sur la figure ci-dessous.
Attention, le repère n'est pas orthonormal.

\includegraphics[

La fonction $ x \rightarrow \mathrm{th}(x)$ est représentée sur la figure ci-dessous.

\includegraphics[

16.7.3 Autres fonctions usuelles

Voir le tableau ci-dessous des dérivées et des développements limités usuels.
On ajoutera la dérivée $ n^{\grave{e}me}$ de$ \sin x$ qui est $ \sin(x+n\dfrac{\pi}{2})$ et celle de $ \cos x$ qui est$ \cos(x+n\dfrac{\pi}{2})$.
On a indiqué l'ensemble de définition de$ f^{\prime}$ quand il différait de celui de $ f$.
Pour les deux dernières qui dépendent d'un paramètre $ a$, on a indiqué les résultat valables pour $ a$ quelconque.

$ f$

D$ _{f}$

$ f'$

$ dl_{n}$

$ \sin x$

$ \mathbb{R}$

$ \cos x=\sin\left(x+\frac{\pi}{2}\right)$

$ \displaystyle\sum_{k=0}^{n}\left( -1\right) ^{k}\dfrac{x^{2k+1}}{\left( 2k+1\right) !}+o\left( x^{2n+2}\right) $

$ \cos x$

$ \mathbb{R}$

$ -\sin x=\cos\left(x+\frac{\pi}{2}\right)$

$ \displaystyle\sum_{k=0}^{n}\left( -1\right) ^{k}\dfrac{x^{2k}}{\left( 2k\right) !}+o\left( x^{2n+1}\right) $

$ \tan x$

$ \left] -\tfrac{\pi}{2},\tfrac{\pi}{2}\right[ +k\pi$, $ k\in\mathbb{Z}$

$ \dfrac {1}{\cos^{2}x}=1+\tan^{2}x$

$ x+\dfrac{x^{3}}{3}+o(x^{4})$

$ \arcsin x$

$ \left[ -1,1\right] $

$ \dfrac{1}{\sqrt{1-x^{2}}}$ $ \left( \left] -1,1\right[ \right) $

$ x+\dfrac{x^{3}}{6}+o(x^{4})$

$ \arccos x$

$ \left[ -1,1\right] $

$ -\dfrac{1}{\sqrt{1-x^{2}}}$$ \left( \left] -1,1\right[ \right) $

$ \dfrac{\pi}{2}-x-\dfrac{x^{3}}{6}+o(x^{4})$

$ \arctan x$

$ \mathbb{R}$

$ \dfrac{1}{1+x^{2}}$

$ \displaystyle\sum _{k=0}^{n}\left( -1\right) ^{k}\dfrac{x^{2k+1}}{\left( 2k+1\right) }+o\left( x^{2n+2}\right) $

$ e^{x}$

$ \mathbb{R}$

$ e^{x}$

$ \displaystyle\sum_{k=0}^{n}\dfrac{x^{k} }{k!}+o\left( x^{n}\right) $

$ \ln x$

$ \left] 0,+\infty\right[ $

$ \dfrac{1}{x}$

 

$ \ln(1+x)$

$ \left] -1,+\infty\right[ $

$ \dfrac{1}{1+x}$

$ \displaystyle \sum_{k=1}^{n}\left( -1\right) ^{k+1}\dfrac{x^{k}}{k}+o\left( x^{n}\right) $

$ \dfrac{1}{1+x}$

$ \mathbb{R}\setminus\{-1\}$

 

$ \displaystyle\sum _{k=0}^{n}\left( -1\right) ^{k}x^{k}+o\left( x^{n}\right) $

$ \ln(1-x)$

$ \left] -\infty,+1\right[ $

$ -\dfrac{1}{1-x}$

$ \displaystyle-\sum_{k=1}^{n}\dfrac{x^{k}}{k}+o\left( x^{n}\right) $

$ \dfrac{1}{1-x}$

$ \mathbb{R}\setminus\{1\}$

 

$ \displaystyle\sum _{k=0}^{n}x^{k}+o\left( x^{n}\right) $

$ \mathrm{ch}\, x$

$ \mathbb{R}$

$ \mathrm{sh}\,x$

$ \displaystyle\sum_{k=0}^{n} \dfrac{x^{2k}}{\left( 2k\right) !}+o\left( x^{2n+1}\right) $

$ \mathrm{sh}\,x$

$ \mathbb{R}$

$ \mathrm{ch}\, x$

$ \displaystyle\sum_{k=0}^{n} \dfrac{x^{2k+1}}{\left( 2k+1\right) !}+o\left( x^{2n+2}\right) $

$ \mathrm{th}\,x$

$ \mathbb{R}$

$ \dfrac{1}{\mathrm{ch}^{2}\,x}=1-\mathrm{th}^{2}\,x$

$ x+o(x^{2})$

$ x^{a}$

$ \left] 0,+\infty\right[ $ ou $ \mathbb{R}$ ou $ \mathbb{R}^{\ast}$

$ a\,x^{a-1}$ $ \left( a\neq0\right) $

 

$ (1+x)^{a}$

$ \left] -1,+\infty\right[ $ ou $ \mathbb{R}$ ou $ \mathbb{R}\setminus\{-1\}$

$ a(1+x)^{a-1}$

$ 1+\displaystyle\sum_{k=1}^{n} \dfrac{a(a-1)\ldots(a-k+1)}{k!}x^{k}+o\left( x^{n}\right) $


© Christophe Caignaert - Lycée Colbert - Tourcoing