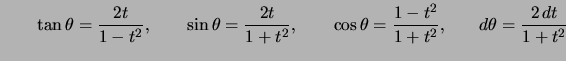Résumé de Cours de Sup et Spé T.S.I.

Rappelons la relation fondamentale de la trigonométrie : $\cos^{2}a+\sin^{2}a=1$ .
La figure ci-dessous représente le cercle trigonométrique.

	0	$\pi /6$	$\pi /4$	$\pi /3$	$\pi /2$
$\sin$	0	1/2	$\sqrt{2}/2$	$\sqrt{3}/2$	1
$\cos$	1	$\sqrt{3}/2$	$\sqrt{2}/2$	1/2	0
$\tan$	0	$\sqrt{3}/3$	1	$\sqrt{3}$	$+\infty$

17.2 Symétries

$\begin{displaymath} \begin{array}[c]{r@{ \,=\, }lcr@{ \,=\, }lcr@{ \,=\, }l} \... ...^{n}\cos x & & \tan\left( x+n\pi\right) & \tan x \end{array} \end{displaymath}$

17.3 Arc double

$\begin{displaymath} \begin{array}[c]{r@{\,=\,}lcr@{\,=\,}lcr@{\,=\,}l} \cos2a ... ...a}{2} & & \tan^{2}a & \dfrac{1-\cos2a}{1+\cos2a} \end{array} \end{displaymath}$

17.4 Sommes d'arcs

$\begin{displaymath} \begin{array}[c]{r@{ \,=\, }lcr@{ \,=\, }l} \sin\left( a+b... ...b\right) & \dfrac{\tan a-\tan b}{1+\tan a\tan b} \end{array} \end{displaymath}$

Notons le cas particulier : $\dfrac{1+ \tan a}{1- \tan a}=\tan \left( a+\dfrac{\pi}{4} \right)$ .

17.5 Transformation de produits en sommes

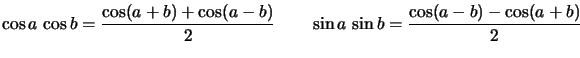
$\cos a \, \cos b = \dfrac{\cos (a+b)+\cos (a-b)}{2} \qquad \sin a \, \sin b = \dfrac{\cos (a-b)-\cos (a+b)}{2}$

17.6 Transformation de sommes en produits

$\begin{displaymath} \begin{array}[c]{r@{ \,=\, }lcr@{ \,=\, }l} \sin p+\sin q ... ...cos q & -2\sin\dfrac{p+q}{2}\sin\dfrac{p-q}{2} \end{array} \end{displaymath}$

17.7 Formule de Moivre

$\left( \cos a+i\sin a\right) ^{n}=\left( e^{ia}\right) ^{n}=e^{ina}=\cos na+i\sin na$

17.8 Fonctions réciproques

$\arcsin:\left[ -1,1\right] \rightarrow\left[ -\dfrac{\pi}{2},\dfrac{\pi}{2}\ri... ...athrm{arctan}:\mathbb{R}\rightarrow\left]-\dfrac{\pi}{2},\dfrac{\pi}{2}\right[$

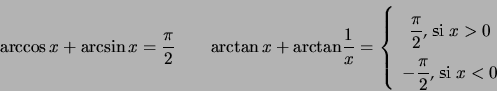
$\begin{displaymath}\arccos x+\arcsin x=\dfrac{\pi}{2}\qquad \mathrm{arctan}\,x+... ...}x>0\\ -\dfrac{\pi}{2}\text{, si }x<0 \end{array} \right. \end{displaymath}$

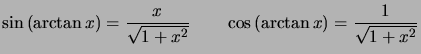
$\sin \left(\mathrm{arctan}\,x\right)=\dfrac{x}{\sqrt{1+x^2}} \qquad \cos \left(\mathrm{arctan}\,x\right)=\dfrac{1}{\sqrt{1+x^2}}$

On a illustré les fonctions trigonométriques réciproques dans la figure ci-dessous.

Remarque : Il faut se méfier des touches des calculatrices qui notent par exemple « $\tan^{-1}$ » l'application réciproque de l'application « $\tan$ », c'est à dire l'application « $\mathrm{arctan}$ » ... Cela provient de ce que l'application « réciproque » est l'application « inverse » pour la composée des applications ...

17.9 Pour le calcul intégral

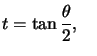Si $t=\tan\dfrac{\theta}{2},\quad$ alors : $\qquad\tan\theta=\dfrac{2t} {1-t^{2}},\qquad\sin\theta=\dfrac{2t}{1+t^{2}},\qquad\cos\theta =\dfrac{1-t^{2}}{1+t^{2}},\qquad d\theta=\dfrac{2\,dt}{1+t^{2}}$

Deuxième Partie : Analyse

17 Trigonométrie