Résumé de Cours de Sup et Spé T.S.I.

Deuxième Partie : Analyse

22 Séries numériques (réelles ou complexes)

Sous-sections


22 Séries numériques (réelles ou complexes)

22.1 Convergence et Convergence Absolue

Définition :   $ \displaystyle\sum u_{n}$ converge $ \Leftrightarrow$ la suite des sommes partielles (s$ _{n})$ avec s$ _{n}=\displaystyle\sum_{k=0}^{n}u_{k}$ converge.

Théorème :   $ \displaystyle\sum\left\vert u_{n}\right\vert $ converge$ \Rightarrow\displaystyle\sum u_{n}$ converge.

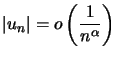Remarque : (règle $ n^{\alpha}u_{n}$)   Si on a $ \alpha>1$ tel que $ \lim \limits_{n\rightarrow\infty}n^{\alpha}u_{n}=0$, alors $ \left\vert u_{n}\right\vert =o\left( \dfrac{1}{n^{\alpha}}\right) $ et donc $ \displaystyle\sum u_{n}$ converge absolument et donc converge.
Ceci n'est pas un théorème et est donc à réargumenter à chaque fois...


22.2 Séries géométriques

Théorème :   La série de terme général $ x^{n}$ converge $ \Leftrightarrow\left\vert x\right\vert <1$. De plus, la somme est :    $ \displaystyle\sum_{n=0}^{\infty}x^{n}=\dfrac{1}{1-x} $

Définition :   Une suite géométrique est une suite vérifiant :    $ \forall n\in\mathbb{N},\quad u_{n+1}=a\,u_n$.$ a$ est la raison de la suite.

Remarque :   La somme d'une série géométrique convergente est donc :    $ \dfrac{\text{<< le premier terme >>}}{1-\text{<< la raison >>}}$.
Ceci prolonge et généralise la somme des termes d'une suite géométrique qui est :

$\displaystyle \dfrac{\text{<< le premier terme >>}-\text{<< le premier terme manquant >>}}{1-\text{<< la raison >>}} $

Quand la série converge, il n'y pas de termes manquants...

22.3 Séries positives

Théorème : (Riemann)       $ u_{n}\underset{+\infty}{\sim}\dfrac{1}{n^{\alpha}} \Rightarrow\left( \displaystyle\sum u_{n} \text{ converge}\Leftrightarrow\alpha>1\right) $

Théorème :   (Comparaison) \begin{displaymath}\left. \begin{array}[c]{r} 0\leqslant u_{n}\leqslant v_{n}\... ...erge} \end{array} \right\} \Rightarrow\displaystyle\sum u_{n}\end{displaymath} converge.

Corollaire :   \begin{displaymath}\left. \begin{array}[c]{r} 0\leqslant u_{n}\leqslant v_{n}\... ...erge} \end{array} \right\} \Rightarrow\displaystyle\sum v_{n}\end{displaymath} diverge.

Théorème :   (Equivalence)\begin{displaymath}\left. \begin{array}[c]{r} 0\leqslant u_{n}\\ u_{n}\under... ...v_{n} \end{array} \right\} \Rightarrow\displaystyle\sum u_{n}\end{displaymath} et $ \displaystyle\sum v_{n}$ sont de même nature.

Théorème :   (d'Alembert) $ \displaystyle\sum u_{n}$ à terme strictement positifs, telle que \begin{displaymath}\lim\limits_{n\rightarrow\infty}\dfrac{u_{n+1}}{u_{n}}=l\quad... ...ent}\\ l=1,\quad\text{on ne sait rien} \end{array} \right. \end{displaymath}

Remarque :   On tombe très souvent sur le cas douteux !
On utilise souvent le théorème de d'Alembert dans le cadre des séries entières, ou lorsqu'on a, dans l'expression de $ u_{n}$, des factorielles, des termes de nature géométrique$ \left( a^{n}\right) $ ou des exponentielles.

22.4 Critère spécial des séries alternées

Définition :   $ \displaystyle\sum u_{n}$ est une série alternée $ \Leftrightarrow \left( -1\right) ^{n}u_{n}$ est de signe constant.

Théorème :   $ \displaystyle\sum u_{n}$ une série alternée     \begin{displaymath}\left. \begin{array}[c]{r} \left( \left\vert u_{n}\right\ve... ...{n}=0 \end{array} \right\} \Rightarrow\displaystyle\sum u_{n}\end{displaymath} converge.
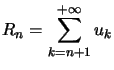De plus, $ \left\vert R_{n}\right\vert \leqslant\left\vert u_{n+1}\right\vert $, où $ R_{n}=\displaystyle\sum _{k=n+1}^{+\infty}u_{k}$, enfin, $ \displaystyle\sum_{k=0}^{+\infty}u_{k}$ est du signe de $ u_{0,}$    $ R_{n}$ est du digne de $ u_{n+1}$

Voir la figure ci-dessous.


\begin{picture}(165,40) \thicklines \put(30,10){\vector(1,0){110}} \thinline... ...+1} \right\vert $} \put(102,22){$\left\vert r_{2n} \right\vert $} \end{picture}

22.5 Comparaison d'une série et d'une intégrale

Théorème :   $ f$ une fonction positive et décroissante définie sur$ \mathbb{R}_{+},\quad\displaystyle\int_{0}^{+\infty}f(t)\,d t$ et $ \displaystyle\sum f(n)$ sont de même nature.
Et si elles convergent :    $ {\displaystyle\int_{n+1}^{+\infty}} f(t)\,d t\leqslant\displaystyle\sum_{k=n+1}^{+\infty}f(k)\leqslant {\displaystyle\int_{n}^{+\infty}} f(t)\,d t$

La figure ci-dessous donne les inégalités de base !
Il ne faut pas hésiter à la refaire pour retouver ces inégalités.

\includegraphics[]{comparaison-serie-integrale}

22.6 Suite et série des différences

Théorème :   La suite $ \left( u_{n}\right) $ converge $ \Leftrightarrow$ La série$ \displaystyle\sum\left( u_{n+1}-u_{n}\right) $ converge

Remarque :   Cela sert parfois à montrer la convergence de quelques ... suites, en montrant la convergence ou la convergence absolue de la série des différences.


22.7 Calcul exact de sommes de séries

On dispose principalement de trois techniques

22.8 Calcul approché de sommes de séries


© Christophe Caignaert - Lycée Colbert - Tourcoing