Définition : Une série entière est une série de la forme ![]() ou
ou ![]() , selon que l'on travaille sur
, selon que l'on travaille sur ![]() ou sur
ou sur ![]()
Pour rechercher le rayon de convergence ![]() ,
,
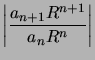 ,
, 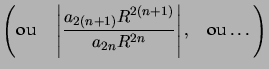 a pour limite 1 quand
a pour limite 1 quand 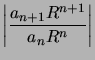 a toujours une limite nulle quand
a toujours une limite nulle quand ![]() , la suite
, la suite ![]() est bornée}
est bornée}
![]() , la suite
, la suite ![]() tend vers 0}
tend vers 0}
La figure ci-dessous illustre ce théorème.

Théorème : Quand la variable est réelle, la série entière se dérive et s'intègre terme à terme sur ![]() au moins.
au moins.
Elle s'intègre même terme à terme au moins sur sur l'intervalle de convergence
Théorème : La série entière, sa série dérivée et ses séries primitives ont le même rayon de convergence.
Théorème : La somme d'une série entière est de classe ![]() sur
sur![]() , et continue sur son ensemble de définition.
, et continue sur son ensemble de définition.
Théorème : ![\begin{displaymath}\left. \begin{array}[c]{l} \displaystyle\sum a_{n}z^{n}\tex... ...t\} \Rightarrow\displaystyle\sum\left( a_{n}+b_{n}\right) z^{n}\end{displaymath}](img781.png) est de rayon
est de rayon![\begin{displaymath}\left\{ \begin{array}[c]{l} \inf(R_{1},R_{2})\text{ pour }R... ...R\geqslant R_{1}\text{ pour }R_{1}=R_{2} \end{array} \right. \end{displaymath}](img782.png)
Définition : Une fonction ![]() est développable en série entière en 0
est développable en série entière en 0![]() il existe une série entière et un intervalle
il existe une série entière et un intervalle ![]() tels que
tels que 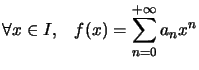
Théorème : Si ![]() est développable en série entière en 0 alors la série entière est la série de Taylor et :
est développable en série entière en 0 alors la série entière est la série de Taylor et : 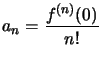
En général ![]() est l'intersection de l'ensemble de définition de
est l'intersection de l'ensemble de définition de![]() et de l'ensemble de convergence de
et de l'ensemble de convergence de 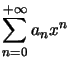 , mais cela n'est pas une obligation...
, mais cela n'est pas une obligation...
Pour développer une fonction en série entière, on peut :
Dans tous les cas, il faudra avec soin justifier la convergence de la série entière et son égalité avec la fonction.
Cela peut être délicat dans le cas de la série de Taylor... qu'on n'utilisera qu'à la demande de l'énoncé.
Voir le tableau ci-dessous des séries entières usuelles.
| D | DSE |
|
|
|---|---|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
La série géométrique et l'exponentielle sont aussi valables pour une variable complexe.
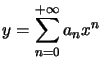 .
.