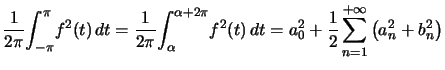Définition : ![]() , T-périodique, continue par morceaux sur
, T-périodique, continue par morceaux sur ![]() , on appelle série de Fourier de
, on appelle série de Fourier de ![]() , la série :
, la série : 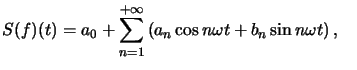 avec :
avec : 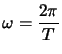
On a  et pour
et pour ![\begin{displaymath}n\geqslant 1, \quad\left\{ \begin{array}[c]{l} a_{n}=\dfrac... ...ha}^{\alpha+T}} f(t)\sin n\omega t\,d t \end{array} \right. \end{displaymath}](img813.png)
Remarque : ![]() est la valeur moyenne de
est la valeur moyenne de ![]() .
.
Dans le cas où ![]() est paire ou impaire, on peut travailler sur une demi-période bien choisie.
est paire ou impaire, on peut travailler sur une demi-période bien choisie.
C'est à dire que, le plus souvent, les intégrales sont calculées entre 0 et ![]() .
.
D'autre part, souvent, on ne dispose d'une formule explicite pour ![]() que sur un certain intervalle.
que sur un certain intervalle.
On veillera avec soin à ne pas utiliser cette formule en dehors de cet intervalle !
Si cela est plus facile, on peut calculer :
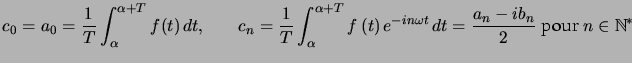
Si la fonction est réelle, les ![]() et
et ![]() sont réels et on les obtient par un seul calcul ...
sont réels et on les obtient par un seul calcul ...
Dans le cas où ![]() est
est ![]() -périodique,
-périodique, 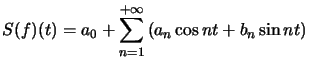
 et pour
et pour ![\begin{displaymath}n\geqslant 1,\quad\left\{ \begin{array}[c]{l} a_{n}=\dfrac{... ...\alpha}^{\alpha+2\pi}} f(t)\sin nt\,d t \end{array} \right. \end{displaymath}](img822.png)
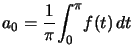 , et pour
, et pour ![\begin{displaymath}n\geqslant1,\quad\left\{ \begin{array}[c]{l} a_{n}=\dfrac{2... ...nt_{0}^{\pi}} f(t)\cos nt\,d t\\ bn=0 \end{array} \right. \end{displaymath}](img824.png)
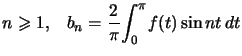
Dans les séries de Fourier, assez souvent, on n'a de formule pour ![]() que dans un certain intervalle, on veillera donc, comme on l'a déjà dit, à n'utiliser cette formule que sur cet intervalle...
que dans un certain intervalle, on veillera donc, comme on l'a déjà dit, à n'utiliser cette formule que sur cet intervalle...
Théorème : (Dirichlet, cas général) ![]() de classe
de classe ![]() par morceaux sur
par morceaux sur ![]() , T-périodique
, T-périodique
![]() la série de Fourier de
la série de Fourier de ![]() converge en tous points, et sa somme est :
converge en tous points, et sa somme est : 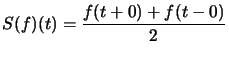
où ![]() et
et ![]() sont les limites à droite et à gauche de
sont les limites à droite et à gauche de ![]() en
en ![]() .
.
Remarque : En tous points où ![]() est continue, on a donc bien :
est continue, on a donc bien : ![]() .
.
Il n'y a qu'aux points où ![]() est discontinue qu'il risque d'y avoir un problème.
est discontinue qu'il risque d'y avoir un problème.
On fera donc un graphe de la fonction sur un peu plus d'une période pour repérer les points de discontinuité et vérifier le caractère![]() par morceaux sur
par morceaux sur ![]() .
.
Théorème : (Dirichlet, cas continu) ![]() continue et de classe
continue et de classe ![]() par morceaux sur
par morceaux sur ![]() , T-périodique
, T-périodique
![]() la série de Fourier de
la série de Fourier de ![]() converge en tous points, et :
converge en tous points, et : ![]() .
.
De plus, les séries ![]() et
et ![]() convergent.
convergent.
Théorème : Sur un intervalle ![]() où
où ![]() est continue
est continue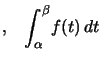 peut se calculer en intégrant terme à terme la série de Fourier de
peut se calculer en intégrant terme à terme la série de Fourier de ![]() .
.
Théorème : (Unicité du développement en série de Fourier) Si ![]() est continue sur
est continue sur ![]() et s'écrit comme la somme d'une série trigonométrique, on a :
et s'écrit comme la somme d'une série trigonométrique, on a :
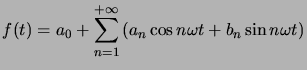
Alors, cette série est la série de Fourier de ![]() .
.
Théorème : ![]() , l'ensemble des applications continues, T-périodiques,
, l'ensemble des applications continues, T-périodiques, ![]() est un espace vectoriel réel.
est un espace vectoriel réel.
De plus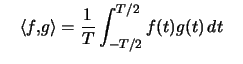 est un produit scalaire de
est un produit scalaire de ![]() .
.
La famille ![]() est orthogonale pour ce produit scalaire.
est orthogonale pour ce produit scalaire.
Remarque : Si les applications sont simplement continues par morceaux ,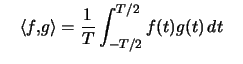 est une forme bilinéaire symétrique positive.
est une forme bilinéaire symétrique positive.
Théorème : (Formule de Parseval) ![]() , T-périodique,continue par morceaux sur
, T-périodique,continue par morceaux sur ![]() , alors :
, alors :
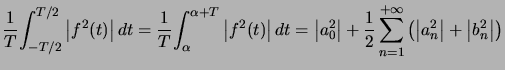
Si la fonction est réelle :
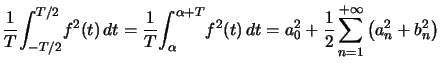
Si, de plus, ![]() est 2
est 2![]() -périodique :
-périodique :