Résumé de Cours de Sup et Spé T.S.I.

Deuxième Partie : Analyse

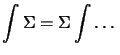
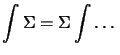
25 $\displaystyle\int\Sigma=\Sigma\displaystyle\int\ldots$

Sous-sections

25 $\displaystyle\int\Sigma=\Sigma\displaystyle\int\ldots$

Problème : Il s'agit de montrer que : ${\displaystyle\int_{a}^{b}} \left( \displaystyle\sum\limits_{n=0}^{+\infty}f_... ...its_{n=0} ^{+\infty}\left( {\displaystyle\int_{a}^{b}} f_{n}(t)\,d t\right)$ .
C'est à dire que l'intégrale d'une série est la série des intégrales.

Le problème n'est jamais évident. Il y a différentes solutions selon les intégrales.
Toutes les justifications doivent se faire avec soin.

25.1 Série entière

Pour une série entière, on peut intégrer terme à terme sur tout intervalle inclus dans l'ouvert de convergence.
Il suffit donc de rappeler qu'on a une série entière et que $\left[ a,b\right] \subset\left] -R,R\right[$

25.2 Série de Fourier

Pour une série de Fourier correspondant à une fonction continue sur $\mathbb{R}$ et de classe $\mathcal{C}^{1}$ par morceaux, on peut également intégrer terme à terme la série.
Il suffit de rappeler ces conditions.

25.3 Autres cas

Que l'intégrale soit une intégrale simple ou une intégrale généralisée le traitement sera le même.
L'idée est de sortir la somme partielle de la série par linéarité, il reste ensuite à montrer que l'intégrale du reste tend bien vers 0.

25.3.1 Utilisation du critère spécial des séries alternées

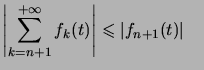
Si à fixé,     $\displaystyle\sum\limits_{n=0}^{+\infty}f_{n}(t)\quad$ converge par application du critère spécial des séries alternées, on a alors :     $\left\vert \displaystyle\sum\limits_{k=n+1}^{+\infty}f_{k}(t)\right\vert \leqslant\left\vert f_{n+1}(t)\right\vert \quad$
Il suffit alors de montrer que     ${\displaystyle\int_{a}^{b}} \left\vert f_{n+1}(t)\right\vert dt\rightarrow0\quad$ quand     $n\rightarrow+\infty$
En effet, on écrit :     ${\displaystyle\int_{a}^{b}} \left( \displaystyle\sum\limits_{n=0}^{+\infty}f_... ...mits_{k=n+1}^{+\infty}f_{k}(t)\right) dt}_{\text{int\'{e}grale du reste}}\quad$ et on majore ce dernier terme en valeur absolue.
Enfin, on passe à la limite sur le terme de droite...

25.3.2 Série géométrique

Si à fixé, la série est géométrique, $\displaystyle\sum_{k=n+1}^{+\infty}f_{k}(t)$ est aussi une série géométrique qui se calcule facilement.
On calcule alors, ou on majore : ${\displaystyle\int_{a}^{b}} \left( \displaystyle\sum\limits_{k=n+1}^{+\infty}f_{k}(t)\right) dt$

25.3.3 Autres cas

Dans les autres cas, l'énoncé doit vous guider. Le principe général est de majorer $\left\vert \displaystyle\sum\limits_{k=n+1} ^{+\infty}f_{k}(t)\right\vert \leqslant g_{n}(t)$ avec ${\displaystyle\int_{a}^{b}} g_{n}(t)\,d t\rightarrow0\quad$ quand $n\rightarrow+\infty\quad$ et d'appliquer le principe précédent. Souvent, on vient de faire une telle majoration dans les questions précédentes...

Remarque : Si l'intégrale est une intégrale généralisée, il ne faut pas oublier de montrer la convergence de toutes les intégrales utilisées.