Résumé de Cours de Sup et Spé T.S.I.

Deuxième Partie : Analyse

26 Fonctions $ \mathbb{R}^{p}\rightarrow\mathbb{R}$

Sous-sections


26 Fonctions $ \mathbb{R}^{p}\rightarrow\mathbb{R}$


26.1 Limite et continuité

Ceci permet de montrer la plupart des continuités usuelles.

Théorème :   Une fonction de plusieurs variables, à valeurs réelles, continue sur un fermé-borné est bornée et atteint ses bornes.

26.2 Classe $ \mathcal{C}^{1}$ et $ \mathcal{C}^{2}$

Définition :   $ f$ est de classe $ \mathcal{C}^{1}$ sur $ \mathcal{U}$ un ouvert de$ \mathbb{R}^{p}\Leftrightarrow f$ admet $ p$ dérivées partielles continues sur $ \mathcal{U}$
Quand ces dérivées partielles sont aussi de classe $ \mathcal{C}^{1}$, on dit que $ f$ est de classe $ \mathcal{C}^{2}$ sur $ \mathcal{U}$

Définition :   Quand $ f$ est de classe $ \mathcal{C}^{1}$ sur $ \mathcal{U}$ un ouvert de$ \mathbb{R}^{3}$, la différentielle de $ f$ en $ (x_{0},y_{0},z_{0})$, est l'application linéaire :

$\displaystyle (\,dx,\,dy,\,dz)\longmapsto \frac{\partial f}{\partial x}(x_{0},y... ...y}(x_{0},y_{0},z_{0})\,dy+\frac{\partial f}{\partial z}(x_{0},y_{0},z_{0})\,dz $

Remarque :   On adapte au besoin cette définition en dimension $ p$...

Théorème :   Si $ f$ est de classe $ \mathcal{C}^{1}$ sur $ \mathcal{U}$ un ouvert de$ \mathbb{R}^{p}$, elle admet un développement limité à l'ordre 1 en tout point de $ \mathcal{U}$ et on a :

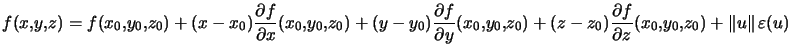
$\displaystyle f(x,y,z)=f(x_{0},y_{0},z_{0})+(x-x_{0})\frac{\partial f}{\partial... ...tial f}{\partial z}(x_{0},y_{0},z_{0})+\left\Vert u\right\Vert \varepsilon(u) $

où    $ u=(x-x_{0},y-y_{0},z-z_{0})$    et    $ \displaystyle\lim_{u\to (0,0,0)}\varepsilon(u)=0$.

Théorème :   (Schwarz)    $ f$ de classe $ \mathcal{C}^{2}$ sur $ \mathcal{U}\Rightarrow \dfrac{\partial^{2}f}{\partial x\partial y}=\dfrac{\partial^{2}f}{\partial y\partial x}$

Théorème : (Fonctions composées)   \begin{displaymath}\left. \begin{array}[c]{r} x,y,z :\quad\mathbb{R}\rightarro... ...ray} \right\} \Rightarrow F\quad\text{est}\quad\mathcal{C}^{1}\end{displaymath} sur I, et $ F^{\prime }(t)=\dfrac{\partial f}{\partial x}\,x^{\prime}(t)+\dfrac{\partial f}{\partial y}\,y^{\prime}(t)+\dfrac{\partial f}{\partial z}\,z^{\prime}(t)$

Remarque :   Si $ x,y,z$ dépendent de 2 ou 3... variables, on a le même résultat en remplaçant toutes les dérivées par des dérivées partielles.


26.3 Extrémums d'une fonction $ \mathbb{R}^{2}\rightarrow\mathbb{R}$

$ (x,y)\to z=f(x,y),\quad$une fonction de classe$ \mathcal{C}^{2}$ sur $ \mathcal{U}$ un ouvert de $ \mathbb{R}^{2}$. Pour chercher ses extrémums :


© Christophe Caignaert - Lycée Colbert - Tourcoing