Résumé de Cours de Sup et Spé T.S.I.

Troisième Partie : Géométrie

32 Courbes et Surfaces

Sous-sections

32 Courbes et Surfaces

32.1 Etude et Tracé de Courbes d'équation

32.1.1 Ensemble d'étude

On recherche l'ensemble de définition, les éventuelles parité ou imparité, la périodicité, pour aboutir à l'ensemble d'étude.
On indiquera alors les transformations à appliquer à l'arc de courbe pour reconstituer la courbe entière.

32.1.2 Etude des variations

L'étude des variations se fait le plus souvent en étudiant le signe de la dérivée, obtenu en utilisant au besoin une fonction auxiliaire.

Remarque : Pour le choix d'une fonction auxiliaire, il faut dans celle ci « isoler » les éventuels

logarithmes,
et arctangentes

qui se transforment en fraction rationnelle quand on dérive.

32.1.3 Limites aux bornes

On cherche les limites à toutes les bornes de l'ensemble d'étude, avec au besoin,

l'étude du prolongement par continuité en cas de limite finie,
et l'étude locale de la dérivabilité en ces points, pour placer la tangente.

32.1.4 Inflexions

L'étude des inflexions se fait au moyen de la dérivée seconde : $\quad f^{\prime\prime} (x_{0})=0\quad$ caractérisent les points où il peut y avoir une inflexion géométrique.
Cette étude n'est faite qu'à la demande de l'énoncé.
Géométriquement, un point d'inflexion se caractérise par le fait que la courbe traverse sa tangente.

32.1.5 Branches infinies

On a une branche infinie quand : $\quad f(x)\rightarrow\pm\infty\quad$ ou $x\rightarrow\pm\infty$

$\lim\limits_{x\rightarrow x_{0}}f(x)=\pm\infty,\quad$ on a une asymptote verticale d'équation : .

$\lim\limits_{x\rightarrow\pm\infty}f(x)=b,\quad$ on a une asymptote horizontale d'équation : .

$\lim\limits_{x\rightarrow\pm\infty}f(x)=\pm\infty$ Il faut continuer la recherche par : $\lim\limits_{x\rightarrow\pm\infty}\dfrac{f(x)}{x}=a$

si $a=\pm\infty ,\quad$ on a une branche parabolique de direction .
si $a=0,\quad$ on a une branche parabolique de direction .
si est fini non nul, il faut continuer la recherche par :
- si est fini, on a une asymptote :
- si est infini, on a une branche parabolique de direction
- si n'a pas de limite, on a une branche infinie de direction asymptotique

32.1.6 Centre de symétrie

Quand est impaire, l'origine est centre de symétrie de la courbe représentative de .
Le point de coordonnées est centre de symétrie de la courbe si et seulement si est constant, il vaut alors .

32.1.7 Convexité

Une fonction 2 fois dérivable est convexe si et seulement si la dérivée seconde est positive.
Géométriquement, une courbe est convexe si et seulement si elle est en dessous de sa corde entre 2 points quelconques ou si et seulement si elle est au dessus de chacune de ses tangentes.
Une fonction convexe a sa concavité tournée vers le haut et une fonction concave a sa concavité tournée vers le bas.
La figure ci-dessous illustre la convexité.

$\includegraphics[width=12cm]{fonction-convexe}$

32.2 Courbes planes en paramétriques

On a : $\begin{displaymath}\left\{ \begin{array}[c]{l} x=f(t)=x(t)\\ y=g(t)=y(t) \end{array} \right. \end{displaymath}$

32.2.1 Ensemble d'étude

On recherche les ensembles de définition, les éventuelles parité ou imparité, les périodicités, pour aboutir à l'ensemble d'étude.
On indiquera alors les transformations à appliquer à l'arc de courbe pour reconstituer la courbe entière.

32.2.2 Variations

On étudie les variations de et . Il faut construire le tableau de variation, qui contient les lignes $x^{\prime }(t)$ , , , $y^{\prime}(t)$ et $\dfrac{y^{\prime}(t)}{x^{\prime }(t)}$ qui représente la pente de la tangente. Remarquons que si $\dfrac{y^{\prime}(t)}{x^{\prime }(t)}$ est une forme indéterminée en un point, on peut la remplacer par sa limite qui représente encore la pente de la tangente.

32.2.3 Points stationnaires

Les points stationnaires vérifient : $\begin{displaymath}\left\{ \begin{array}[c]{l} x^{\prime}(t_{0})=0\\ y^{\prime}(t_{0})=0 \end{array} \right. \end{displaymath}$ On appelle alors :

, avec $p\geqslant 1, \quad$ le premier rang où $\begin{displaymath}\left( \begin{array}[c]{l} x^{(p)}(t_{0})\\ y^{(p)}(t_{0}) \end{array} \right) \end{displaymath}$ est non nul, ce vecteur est alors tangent à la courbe.
, avec $q>p, \quad$ le premier rang où $\begin{displaymath}\left( \begin{array}[c]{l} x^{(q)}(t_{0})\\ y^{(q)}(t_{0}) \end{array} \right) \end{displaymath}$ est non colinéaire à $\begin{displaymath}\left( \begin{array}[c]{l} x^{(p)}(t_{0})\\ y^{(p)}(t_{0}) \end{array} \right) \end{displaymath}$

La courbe est toujours tangente à $\overrightarrow{F^{\left( p\right) }\left( t_{0}\right) }$ , la parité de donne le signe de la coordonnée lorsque $t<t_{0}$ , la parité de donne dans ce cas le signe de la deuxième coordonnée.
Dans les figures suivantes, le repère tracé est : $\left( M_{0},\overrightarrow{F^{\left( p\right) }\left( t_{0}\right) },\overrightarrow{F^{\left( q\right) }\left( t_{0}\right) }\right)$ . On peut voir sur la figure ci-dessous l'ensemble des cas.

$\textstyle \parbox{2.6515in}{\begin{center} \includegraphics[ height=1.3136in... ...mpair} \textbf{et} $q$\ \textbf{pair} \textbf{: point ordinaire} \end{center}}$ $\textstyle \parbox{2.6057in}{\begin{center} \includegraphics[ height=1.3136in... ...} \textbf{et} $q$\ \textbf{impair} \textbf{: point d'inflexion} \end{center}}$
$\textstyle \parbox{2.6057in}{\begin{center} \includegraphics[ height=1.3136in... ...broussement de }$\mathbf{1}^{\grave{e}re}$\ \textbf{esp\\lq {e}ce} \end{center}}$ $\textstyle \parbox{2.6057in}{\begin{center} \includegraphics[ height=1.3136in... ...broussement de }$\mathbf{2}^{\grave{e}me}$\ \textbf{esp\\lq {e}ce} \end{center}}$

Remarquons que si la tangente est verticale ou horizontale, le calcul de est inutile, les variations permettent alors de déterminer directement la nature du point.

32.2.4 Points d'inflexion

Les points d'inflexion géométrique vérifient nécessairement $\begin{displaymath}\left\vert \begin{array}[c]{ll} x^{\prime} & x^{\prime\prime}\\ y^{\prime} & y^{\prime\prime} \end{array} \right\vert =0\end{displaymath}$ .
On ne fait cette étude qu'à la demande de l'énoncé.

32.2.5 Branches infinies

L'étude des branches infinies ne pose de problème qu'au cas où et tendent vers l'infini.

Si $y(t)\rightarrow\pm\infty$ , et $x\left( t\right) \rightarrow l$ , quand $t\rightarrow t_{0}$ : on a une asymptote verticale d'équation .
Si $x(t)\rightarrow\pm\infty$ , et $y\left( t\right) \rightarrow l$ , quand $t\rightarrow t_{0}$ : on a une asymptote horizontale d'équation .
Si et , quand , on calcule appelée :
- si il n'y a pas de limite, on ne dit rien de plus,
- si $a=\pm\infty ,\quad$ on a une branche parabolique de direction ,
- si $a=0,\quad$ on a une branche parabolique de direction ,
- dans les autres cas, on calcule appelée :
  - si il n'y a pas de limite, on a une branche infinie de direction asymptotique
  - si $b=\pm\infty ,\quad$ on a une branche parabolique de direction
  - dans les autres cas, on a une asymptote

32.3 Courbes planes en polaires

Il s'agit d'étudier les courbes définies en coordonnées polaires par : $\rho=f(\theta)=\rho(\theta)$

32.3.1 Ensemble d'étude

On cherche l'ensemble de définition, la périodicité éventuelle, on obtient un premier intervalle : celui-ci doit être un multiple de la période et de $2\pi$ .
On cherche ensuite à réduire cet intervalle.
On essaye de comparer $\rho\left( \theta\right)$ à : $\rho\left( -\theta\right)$ , $\rho(\theta+\pi)$ , $\rho(\pi-\theta)$ , et $\rho(\dfrac{\pi}{2}-\theta)$ .
On en déduit l'ensemble d'étude et d'éventuelles symétries de la courbe.

32.3.2 Variations

On ne fait l'étude des variations de $\rho$ par le signe de $\rho^{\prime}$ que sisi cette étude est simple !
On peut très bien s'en passer pour tracer la courbe.

32.3.3 Signe de $\rho$

L'étude du signe de $\rho$ est par contre indispensable.
Elle qui figure dans le tableau de « variations » et permet de déterminer dans quel cadran on trace la courbe.

Remarque : Notons bien que, dans l'étude des courbes en polaires, $\rho$ peut être négatif.

La figure ci-dessous montre un exemple de $\rho$ négatif.

$\includegraphics[$

32.3.4 Tangentes

On étudie la tangente en quelques points particuliers, en utilisant : $\tan V=\dfrac{\rho}{\rho^{\prime}}$ , qui fournit l'angle, orienté, entre le rayon vecteur et la tangente.
En un point où $\rho(\theta_{0})=0$ , la tangente à la courbe est toujours la droite $\theta=\theta_{0}$ .
La figure déjà vue, et la figure ci-dessous précisent les angles utilisés.

$\includegraphics[]{tangente-polaires}$

32.3.5 Branches infinies

Pour l'étude des branches infinies, on cherche : $\lim\limits_{\theta \rightarrow\theta_{0}}\rho(\theta)\sin\left( \theta-\theta_{0}\right)$ , qui est dans le repère tourné de $\theta_{0}$ .
Tout se passe maintenant dans le repère tourné de $\theta_{0}$ .

s'il n'y a pas de limite, on a une branche infinie de direction asymptotique
cette limite est infinie, on a une branche parabolique de direction
cette limite est finie $Y_{0}$ , on a une asymptote d'équation $Y=Y_{0}$ La figure ci-dessous indique la position de l'asymptote.

$\includegraphics[width=6in]{asymptote-polaires}$

32.3.6 Points d'inflexion

On cherche les points d'inflexion parmi les points où la courbure est nulle. Ce sont les points qui vérifient : $\rho^{2}+2\rho^{\prime2}-\rho \rho^{\prime\prime}=0$ .
On ne fait cette étude qu'à la demande de l'énoncé.

32.4 Courbes usuelles en polaires

On a les coniques d'équation $\rho=\dfrac{p}{1+e\cos\theta}$ Voir page .
$\rho=\dfrac{A}{\cos\left( \theta-\theta_{0}\right) }\quad$ est une droite $\Delta$
$\rho=A\cos\left( \theta-\theta_{0}\right) \quad$ est le cercle passant par de diamètre et de centre sur la droite $\theta=\theta_{0}$

32.5 Surfaces, plan tangent

Une surface peut être définie par une équation cartésienne : ou sous forme de nappe paramètrée : $\begin{displaymath}\left\{ \begin{array}[c]{l} x=f(u,v)\\ y=g(u,v)\\ z=h(u,v) \end{array} \right. \end{displaymath}$
On passe d'une représentation paramétrique à une représentation cartésienne en éliminant les 2 paramètres entre les 3 équations.
On obtient l'équation d'une surface qui contient la nappe paramétrée.
Pour savoir si on a ajouté des points, il faut chercher si pour un point de la surface on peut retrouver les valeurs des paramètres qui correspondent à ce point.

32.5.1 Plan tangent à une surface définie en cartésiennes

Pour le plan tangent à d'équation : $F(x,y,z)=0\quad$ en $\begin{displaymath}\left( \begin{array}[c]{l} x_{0}\\ y_{0}\\ z_{0} \end{array} \right) \end{displaymath}$ , on se place dans le cas où est de classe $\mathcal{C}^{1}$ au moins.
Le vecteur $\begin{displaymath}\left( \begin{array}[c]{l} \dfrac{\partial F}{\partial x}(x... ...artial F}{\partial z}(x_{0},y_{0},z_{0}) \end{array} \right) \end{displaymath}$ est normal à la surface (repère orthonormal), si ce vecteur est non nul, le plan tangent est donc d'équation : $\left( X-x_{0}\right) \dfrac{\partial F}{\partial x}+\left( Y-y_{0}\right) \d... ...artial F}{\partial y}+\left( Z-z_{0}\right) \dfrac{\partial F}{\partial z}=0$ .

32.5.2 Plan tangent à une nappe paramétrée

Pour le plan tangent à la nappe paramètrée :     $\begin{displaymath}\left\{ \begin{array}[c]{l} x=f(u,v)\\ y=g(u,v)\\ z=h(u,v) \end{array} \right. \quad\end{displaymath}$ en $\begin{displaymath}\left( \begin{array}[c]{l} x_{0}\\ y_{0}\\ z_{0} \end{array} \right) \end{displaymath}$ correspondant à $(u_{0},v_{0})$ , on se place dans le cas où sont de classe $\mathcal{C}^{1}$ au moins.
Les vecteurs :     $\begin{displaymath}\left( \begin{array}[c]{l} \dfrac{\partial f}{\partial u}(u... ...rac{\partial h}{\partial u}(u_{0},v_{0}) \end{array} \right) \end{displaymath}$     et     $\begin{displaymath}\left( \begin{array}[c]{l} \dfrac{\partial f}{\partial v}(u... ...rac{\partial h}{\partial v}(u_{0},v_{0}) \end{array} \right) \end{displaymath}$     définissent la direction du plan tangent s'ils forment une famille libre.
Le plan tangent est donc normal au produit vectoriel :     $\begin{displaymath}\left( \begin{array}[c]{l} \dfrac{\partial f}{\partial u}\\... ...al v}\\ \dfrac{\partial h}{\partial v} \end{array} \right) \end{displaymath}$ .
Si ce produit vectoriel n'est pas nul, le plan tangent est donc d'équation :     $\begin{displaymath}\left\vert \begin{array}[c]{ccc} \left( X-x_{0}\right) & \d... ... & \dfrac{\partial h}{\partial v} \end{array} \right\vert =0\end{displaymath}$
Le plan tangent à une surface est visualisé figure ci-dessous.

$\includegraphics[]{Plan-Tangent}$

32.6 Tangente à une courbe de l'espace

Une courbe de l'espace peut être définie par une intersection de surfaces : $\begin{displaymath}\left\{ \begin{array}[c]{l} F(x,y,z)=0\\ G(x,y,z)=0 \end{array} \right. \end{displaymath}$ ou sous forme de représentation paramètrique : $\begin{displaymath}\left\{ \begin{array}[c]{l} x=f(u)\\ y=g(u)\\ z=h(u) \end{array} \right. \end{displaymath}$

Dans le cas d'une intersection de surfaces, l'intersection des plans tangents, si elle est une droite, est la tangente à la courbe au point considéré.
Dans le cas d'une représentation paramétrique, le vecteur $\begin{displaymath}\left( \begin{array}[c]{l} f^{\prime}(u_{0})\\ g^{\prime}(u_{0})\\ h^{\prime}(u_{0}) \end{array} \right) \end{displaymath}$ , s'il est non nul, dirige la tangente qui est donc de représentation paramétrique $\begin{displaymath}\left\{ \begin{array}[c]{l} X=x_{0}+\lambda\, f^{\prime}(u_... ...\\ Z=z_{0}+\lambda\, h^{\prime}(u_{0}) \end{array} \right. \end{displaymath}$

32.7 Rayon de courbure d'une courbe plane

Définition : , l'abscisse curviligne dans le sens des ou $\theta$ croissants vérifie, selon les cas :

$\displaystyle \,ds=\sqrt{x^{\prime2}(t)+y^{\prime2}(t)}\,dt=\sqrt{\rho^{2}+\rho^{\prime2} }\,d\theta$

Définition : $\left( \Omega,\overrightarrow{T},\overrightarrow{N}\right)$ est le repère de Frenet au point $\Omega$ avec : $\overrightarrow{T}=\dfrac{\,d\overrightarrow{OM}}{\,ds}=\dfrac{\dfrac {\,d\ov... ...row{OM}}{\,dt}}{\left\Vert \dfrac{\,d\overrightarrow{OM}}{\,dt}\right\Vert }$ et $\left( \overrightarrow{T},\overrightarrow{N}\right)$ est orthonormal direct.

Définition : Le rayon de courbure , la courbure $\gamma$ sont donnés par : $\dfrac{\,d\overrightarrow{T}}{\,ds}=\gamma\overrightarrow{N}=\dfrac{1} {R}\overrightarrow{N}$ et on a aussi : $\dfrac{\,d\overrightarrow{N}}{\,ds}=-\gamma\overrightarrow{T}=-\dfrac{1} {R}\overrightarrow{T}$

Remarque :

$R>0,\quad$ on tourne à gauche (la courbe est orientée)
$R<0,\quad$ on tourne à droite.

La convention est différente de celle des physiciens pour lesquels est le rayon de courbure géométrique, c'est à dire qu'on a toujours, en physique, .

Définition : Le centre de courbure $\Omega$ est donné par : $\Omega =M+R\overrightarrow {N}$

La figure ci-dessous donne l'ensembles des éléments géométriques

$\includegraphics[$

32.8 Recherche de la courbure

Dans le cas paramétrique ou en polaire, il est utile de considérer la fonction angulaire associée $\varphi$ qui est l'angle entre et $\overrightarrow{T}$ d'où,

en paramétriques, $\begin{displaymath}\overrightarrow{T}:\left( \begin{array}[c]{l} \cos\varphi\\... ...c{\,dy}{\,dt}}/{\dfrac{\,ds}{\,dt}} \end{array} \right) \quad\end{displaymath}$ et $\begin{displaymath}\overrightarrow{N}:\left( \begin{array}[c]{l} -\sin\varphi\\ \cos\varphi \end{array} \right) \end{displaymath}$
en polaires, on a : $\quad\varphi=\theta+V$

Théorème : Pour calculer la courbure ou le rayon de courbure, on utilise le plus souvent :

$\displaystyle \gamma=\dfrac{\,d\varphi}{\,ds}$ ou bien $\displaystyle \quad R=\dfrac{\,ds}{\,d\varphi}$

En paramétriques, on peut parfois « reconnaître » directement la fonction $\varphi(t)$ à partir des expressions de $\overrightarrow{T}$ .
Si on ne reconnait pas cette fonction, on a : $\quad\tan\varphi=\dfrac{y^{\prime }}{x^{\prime}}$ , donc : $\quad\left( 1+\tan^{2}\varphi\right) \dfrac{\,d\varphi}{\,dt}=\left( \dfrac{y^{\prime}}{x^{\prime}}\right) ^{\prime }\quad$ permet d'avoir $\dfrac{\,d\varphi}{\,dt}$
Alors, $\quad R=\dfrac{\,ds}{\,d\varphi}=\dfrac{\frac{\,ds}{\,dt}}{\frac{\,d\varphi}{\,dt} }\quad$ qui se calcule facilement.
En polaires, $\quad\varphi=\theta+V\quad$ avec $\tan V=\dfrac{\rho}{\rho^{\prime}}$ , donc $\dfrac{\,d\varphi}{\,d\theta}=1+\dfrac{\,dV} {\,d\theta}\quad$ se calcule facilement et : $R=\dfrac{\,ds}{\,d\varphi}=\dfrac{\frac{\,ds}{\,d\theta}}{\frac{\,d\varphi}{\,d\theta}}$

32.8.1 Formules directes

On peut aussi rechercher, si on aime les calculs, des formules directes donnant courbure et rayon de courbure.
Cela est parfois utile quand on cherche les éléments de courbure pour une valeur particulière du paramètre.

En paramétriques :
En cartésiennes : , on considère qu'on a une courbe paramétrée par $\begin{displaymath}\left\{ \begin{array}[c]{c} x=x\\ y=f(x) \end{array} .\right. \end{displaymath}$
Ceci évite d'avoir à mémoriser de nouvelles formules...
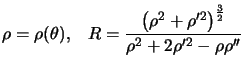
En polaires : $\rho=\rho(\theta), \quad R=\dfrac{\left( \rho^{2} +\rho^{\prime2}\right) ^{\frac{3}{2}}}{\rho^{2}+2\rho^{\prime2}-\rho \rho^{\prime\prime}}$

32.8.2 Pour la valeur 0 du paramètre

Un simple développement limité fournit, par la formule de Taylor :

en paramétriques, appliqué à et , les valeurs de , , et nécessaires au calcul de la courbure.
en polaires, appliqué à $\rho(\theta)$ les valeurs de $\rho(0)$ , $\rho'(0)$ et $\rho''(0)$ qui donnent aussi facilement la courbure.