|
|
| |
|
| ||
|
|
| |
|
| ||
On travaille toujours dans un repère orthonormal.
![\begin{displaymath}\Omega:\left( \begin{array}[c]{c} x_{0}\\ y_{0} \end{array} \right) \end{displaymath}](img1157.png)
et de rayon 
est d'équation : 
est d'équation : 
![\begin{displaymath}\Omega:\left( \begin{array}[c]{c} x_{0}\\ y_{0}\\ z_{0} \end{array} \right) \end{displaymath}](img1161.png)
et de rayon est d'équation : 
est d'équation : Théorème : (Angle au centre) 
et 
distincts appartiennent à un même cercle de centre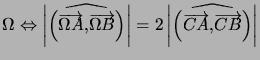 
Théorème : 
et 
distincts sont cocycliques ou alignés![$ \Leftrightarrow\widehat{\left( \overrightarrow{AC},\overrightarrow {BC}\right... ... \pi\right] }\widehat{\left( \overrightarrow {AD},\overrightarrow{BD}\right) }$](img1165.png)
Théorème : Si 
sont les affixes de 
distincts dans le plan complexe, et appartiennent à un même cercle ou sont alignés![$ \Leftrightarrow\arg\left( \dfrac{c-b}{c-a}\right) =_{\left[ \pi\right] }\arg\left( \dfrac{d-b}{d-a}\right) $](img1168.png)
Le plus souvent, un cercle dans l'espace est donné par l'intersection d'une sphère et d'un plan.
Cette intersection est un cercle, un point ou vide selon la distance du centre de la sphère au plan.
On appelle axe du cercle la droite perpendiculaire au plan passant par le centre de la sphère.
Remarque : L'intersection de deux sphères, selon la distance des centres par rapport à la somme des rayons, est aussi un cerle, un point ou vide.
